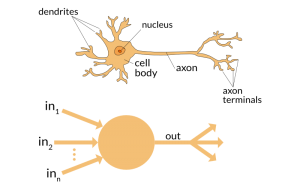
Az alábbi képen a biológiai neuront és annak mesterséges intelligencia modellekben használt analógját látjuk. A biológiai neuron az emberi agy alapvető építőeleme, amely információkat dolgoz fel és továbbít más neuronok felé. A neuron dendritekkel rendelkezik, amelyek a környező neuronoktól érkező jeleket fogadják. Ezeket a jeleket a sejt (amelyben a mag található) dolgozza fel, majd továbbküldi az axonon keresztül. Az axon végén található axon-végződések szinapszisokon keresztül kapcsolódnak más neuronokhoz, így biztosítva az információáramlást.

A mesterséges neuron, a fenti biológiai modell alapján működik, leegyszerűsítve annak alapvető működését. A mesterséges neuron bemeneteket fogad, amelyeket (matematikailag) súlyoz (ezzel vezérli a bemenet fontosságát), majd összegez. Az így kapott értéken egy aktivációs függvényt futtat, amely meghatározza, hogy a neuron “tüzel-e”, azaz továbbküldi-e a jelet. Az aktivációs függvény eredménye képezi a neuron kimenetét, amelyet továbbít a hálózat következő rétegeinek.

Az alábbi kép egy mesterséges neurális hálózat egyszerű modelljét ábrázolja.

A hálózat bemeneti réteggel indul, amely a zöld színű x₁ és x₂ elemeket tartalmazza. Ezek a bemeneti változók képviselik azokat az adatokat, amelyeket a modell feldolgoz. A bemeneteket súlyokkal szorozzák, majd átadják a rejtett rétegek neuronjaiba, amelyeket a kék színű z₁, z₂ és z₃ jelöl.

A rejtett réteg(ek)ben minden neuron kiszámítja a saját kimenetét egy aktivációs függvény segítségével, amely a bemeneti jelek összegét alakítja át (nemlineáris módon). Ezek a kimenetek aztán tovább haladnak a következő rétegekbe (a példában csak 1 rejtett réteget használunk, ezért itt nincs továbbadás), míg végül elérik a kimeneti réteget, amelyet itt az y_pred (y predikció) narancssárga elem jelöl.

Az y_pred a modell végső előrejelzése, egy számérték, amely például egy osztályozási vagy regressziós (közelítési) probléma megoldásaként jelenik meg.

Ez az ábra segít megérteni a neurális hálózatok alapvető működési elvét: a bemenetek fokozatos átalakulását a különböző rétegeken keresztül, amelyek végül egy konkrét kimeneti értékhez vezetnek. Ezt a folyamatot a gépi tanulás során finoman hangolják (optimalizálják), például visszaterjesztés (backpropagation) és gradienscsökkentés (gradient descent) segítségével, hogy a modell pontos előrejelzéseket tudjon adni.

Ha egy kép a bement, akkor a pixeleit sorban is be lehet adni a hálónak (nem vesszük figyelembe, hogy a kép téglalap). A finomhangolás során - a bemutatott minták alapján - a háló megtanulja a pixelek közötti összefüggéseket, és választ tud majd adni, hogy mosolyog-e a képen látható személy, egy olyan képen is, amit korábban nem mutattak meg a hálónak (a modellnek). Megjegyzés: olyan modellek természetesen jobban működnek, amik figyelembe veszik a szomszédos pixeleket is (pl. konvolúciós hálok).

Az ábrán, a fully-connected layer azt jelenti, hogy a minden bementi neuron minden a következő réteg minden neuronjával össze van kapcsolva.

A neurális hálót, az összeköttetéseihez rendelt súlyok segítségével tudjuk használni. A bementből és a rejtett réteg két neuronjának \(z_1\) és \(z_2\) értékét az alábbi képlettel számolhatjuk:

$$ z_1 = x_1 \cdot w_{11} + x_2 \cdot w_{21} $$ $$ z_2 = x_1 \cdot w_{12} + x_2 \cdot w_{22} $$

A rejtett réteg teljesen összekötött (fully connected), ezért minden bemenet kapcsolódik minden rejtett neuronhoz.

A következő kimeneti réteg \(z_3 = y_{pred}\) értékét, ami egyetlen neuronból áll így számíthatjuk:

$$ z_3 = z_1 \cdot w_{31} + z_2 \cdot w_{32} $$

Egyben ez lesz a háló előrejelzése \(y_{\text{pred}}\). Ezt a fenti műveletet forward pass-nak nevezzük.

Az egységesítés és a könnyebb kezelhetőség miatt, a fenti képleteket mátrixos és vektoros formában is felírhatjuk:

Rejtett réteg súlymátrixa: \( W_1 = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix}\)

A kimeneti réteg vektor: \( W_2 = \begin{bmatrix} w_{31} \\ w_{32} \end{bmatrix}\)

Bemeneti és rejtett réteg vektorok: \( \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} , \quad \mathbf{z} = \begin{bmatrix} z_1 \\ z_2 \end{bmatrix}\)

Ezek alapján a rejtett réteget a bement és a súlymátrix alapján így számolhatjuk:

$$ \mathbf{z} = W_1 \cdot \mathbf{x} $$ behelyettesítve: $$ \begin{bmatrix} z_1 \\ z_2 \end{bmatrix} = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $$

A kimenet eredménye egy számérték (skalár) lesz:

$$ y_{\text{pred}} = \begin{bmatrix} w_{31} \\ w_{32} \end{bmatrix} \cdot \begin{bmatrix} z_1 \\ z_2 \end{bmatrix}$$

Teljes mátrixos formában:

$$ y_{\text{pred}} = W_2 \cdot W_1 \cdot \mathbf{x} $$

Tegyük fel hogy:

$$ W_1 = \begin{bmatrix} 0.5 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} , \quad W_2 = \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix} , \quad \mathbf{x} = \begin{bmatrix} 0.8 \\ 0.6 \end{bmatrix}$$

Rejtett réteg számítása:

$$ \mathbf{z} = \begin{bmatrix} 0.5 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} \cdot \begin{bmatrix} 0.8 \\ 0.6 \end{bmatrix} = \begin{bmatrix} (0.5 \cdot 0.8 + 0.3 \cdot 0.6) & (0.2 \cdot 0.8 + 0.7 \cdot 0.6) \end{bmatrix} = \begin{bmatrix} 0.58 \\ 0.58 \end{bmatrix}$$

Kimeneti réteg számítása:

$$ y_{\text{pred}} = \begin{bmatrix} 0.58 \\ 0.58 \end{bmatrix} \cdot \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix} = (0.52 \cdot 0.6 + 0.66 \cdot 0.4) = 0.58 $$

“Loss” a neurális háló teljesítményének mérésére szolgáló függvény, amely azt jelzi, hogy a háló által számolt kimenetek mennyire térnek el a várt kimenetektől.

$$ \text{Loss} = \frac{1}{2} (y - y_{pred})^2 $$

A back-propagation során a Loss függvény deriváltját (gradiensét) használjuk a súlyok frissítéséhez.

$$ \frac{\partial \text{Loss}}{\partial w_{31}} = \frac{\partial \text{Loss}}{\partial y_{\text{pred}}} \cdot \frac{\partial y_{\text{pred}}}{\partial w_{31}} $$

---

1.) Első tényező: \( \frac{\partial \text{Loss}}{\partial y_{\text{pred}}} \) a Loss függvény deriváltja a \(y_{pred}\)-re:

$$ \frac{\partial \text{Loss}}{\partial y_{\text{pred}}} = -(y_{\text{true}} - y_{\text{pred}}) = -e $$

ahol \( e = y - y_{\text{pred}} \) a hiba.

---

2.) Második tényező: \( \frac{\partial y_{\text{pred}}}{\partial w_{31}} \)

Az \(y_{pred}\) függ a rejtett kimenettől \(z_1\):

$$ y_{\text{pred}} = z_1 \cdot w_{31} + z_2 \cdot w_{32} $$

Ezért:

$$ \frac{\partial y_{\text{pred}}}{\partial w_{31}} = z_1 $$

Teljes derivált:

Összekapcsolva a két tényezőt:

$$ \frac{\partial \text{Loss}}{\partial w_{31}} = -e \cdot z_1 $$

hasonlóan:

$$ \frac{\partial \text{Loss}}{\partial w_{32}} = -e \cdot z_2 $$

---

3.) Gradiens a kimeneti súlyokra \(W_2\)

A súlyok gradiensének mátrixos formája:

$$ \Delta W_2 = \begin{bmatrix} \frac{\partial \text{Loss}}{\partial w_{31}} \\ \frac{\partial \text{Loss}}{\partial w_{32}} \end{bmatrix} = \begin{bmatrix} z_1 \cdot e \\ z_2 \cdot e \end{bmatrix}$$

A kimeneti réteg hibáját \(e\) visszaterjesztjük a rejtett réteg neuronjaira (\(h_1, h_2\)):

$$ \delta_{\text{hidden}} = \begin{bmatrix} e \cdot w_{31} \\ e \cdot w_{32} \end{bmatrix}$$

Ez a rejtett réteg hibája.

A bemeneti réteg és a rejtett réteg közötti súlyok gradiensét a bemenetek \(x\) és a rejtett réteg hibájának (\(\delta_{\text{hidden}}\)) szorzata adja:

$$ \Delta W_1 = \begin{bmatrix} x_1 \cdot \delta_{z_1} & x_1 \cdot \delta_{z_2} \\ x_2 \cdot \delta_{z_1} & x_2 \cdot \delta_{z_2} \end{bmatrix}$$

ahol: \( \delta_{z_1} = e \cdot w_{31}, \quad \delta_{z_2} = e \cdot w_{32} \)

---

A súlyok frissítését a gradiensek \(\Delta W_1, \Delta W_2\) és a tanulási ráta \(\eta\) segítségével frissítjük:

$$ W_1 = W_1 - \eta \cdot \Delta W_1 $$ $$ W_2 = W_2 - \eta \cdot \Delta W_2 $$

A teljes eljárás c implementációja:

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

// Adatok (bemenetek és várt kimenetek)
#define INPUT_NODES 2
#define HIDDEN_NODES 2
#define OUTPUT_NODES 1
#define SAMPLES 3
#define EPOCHS 1000
#define LEARNING_RATE 0.01

// Adatok és súlyok inicializálása
double inputs[SAMPLES][INPUT_NODES] = {
    {0.3, 0.1},
    {0.8, 0.6},
    {0.5, 0.5}
};
double expected_outputs[SAMPLES][OUTPUT_NODES] = {
    {0.2},
    {0.7},
    {0.5}
};

// Súlyok
double weights_input_to_hidden[INPUT_NODES][HIDDEN_NODES];
double weights_hidden_to_output[HIDDEN_NODES][OUTPUT_NODES];

// Véletlen szám generálása 0 és 1 között
double random_double() {
    return (double)rand() / RAND_MAX;
}

// Forward pass függvény: Egyetlen minta alapján kiszámítja a kimenetet
void forward_pass(double *input, double *hidden_output, double *final_output,
                  double *weights_input_to_hidden, double *weights_hidden_to_output) {
    // 1. Bemenet -> Rejtett réteg
    for (int i = 0; i < HIDDEN_NODES; i++) {
        hidden_output[i] = 0.0;
        for (int j = 0; j < INPUT_NODES; j++) {
            hidden_output[i] += input[j] * weights_input_to_hidden[j * HIDDEN_NODES + i];
        }
    }

    // 2. Rejtett réteg -> Kimeneti réteg
    for (int i = 0; i < OUTPUT_NODES; i++) {
        final_output[i] = 0.0;
        for (int j = 0; j < HIDDEN_NODES; j++) {
            final_output[i] += hidden_output[j] * weights_hidden_to_output[j * OUTPUT_NODES + i];
        }
    }
}

// Súlyok frissítése
void update_weights(double *weights, double *gradients, int rows, int cols) {
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            weights[i * cols + j] += LEARNING_RATE * gradients[i * cols + j];
        }
    }
}

int main() {
    // Véletlenszerű súlyok inicializálása
    for (int i = 0; i < INPUT_NODES; i++) {
        for (int j = 0; j < HIDDEN_NODES; j++) {
            weights_input_to_hidden[i][j] = random_double();
        }
    }
    for (int i = 0; i < HIDDEN_NODES; i++) {
        for (int j = 0; j < OUTPUT_NODES; j++) {
            weights_hidden_to_output[i][j] = random_double();
        }
    }

    double hidden_layer_output[HIDDEN_NODES];
    double output[OUTPUT_NODES];
    double error[OUTPUT_NODES];

    // Tanítási ciklus
    for (int epoch = 0; epoch < EPOCHS; epoch++) {
        double total_loss = 0.0;

        for (int sample = 0; sample < SAMPLES; sample++) {
            // 1. Forward pass egy mintára
            forward_pass((double *)inputs[sample], hidden_layer_output, output,
                         (double *)weights_input_to_hidden, (double *)weights_hidden_to_output);

            // 2. Hibaszámítás
            for (int i = 0; i < OUTPUT_NODES; i++) {
                error[i] = expected_outputs[sample][i] - output[i];
                total_loss += error[i] * error[i];
            }

            // 3. Visszaterjesztés (backpropagation)
            double gradients_hidden_to_output[HIDDEN_NODES][OUTPUT_NODES] = {0};
            for (int i = 0; i < HIDDEN_NODES; i++) {
                for (int j = 0; j < OUTPUT_NODES; j++) {
                    gradients_hidden_to_output[i][j] = hidden_layer_output[i] * error[j];
                }
            }

            double gradients_input_to_hidden[INPUT_NODES][HIDDEN_NODES] = {0};
            for (int i = 0; i < INPUT_NODES; i++) {
                for (int j = 0; j < HIDDEN_NODES; j++) {
                    double back_error = 0.0;
                    for (int k = 0; k < OUTPUT_NODES; k++) {
                        back_error += error[k] * weights_hidden_to_output[j * OUTPUT_NODES + k];
                    }
                    gradients_input_to_hidden[i][j] = inputs[sample][i] * back_error;
                }
            }

            // 4. Súlyok frissítése
            update_weights((double *)weights_hidden_to_output, (double *)gradients_hidden_to_output, HIDDEN_NODES, OUTPUT_NODES);
            update_weights((double *)weights_input_to_hidden, (double *)gradients_input_to_hidden, INPUT_NODES, HIDDEN_NODES);
        }

        // Hiba kiírása minden epoch után
        if (epoch % 100 == 0) {
            printf("Epoch %d, Loss: %.4f\n", epoch, total_loss / SAMPLES);
        }
    }

    // Eredmények kiírása tanító adatokon
    printf("\nVégső kimenetek tanítás után:\n");
    for (int sample = 0; sample < SAMPLES; sample++) {
        forward_pass((double *)inputs[sample], hidden_layer_output, output,
                     (double *)weights_input_to_hidden, (double *)weights_hidden_to_output);

        printf("Bemenet: [%.2f, %.2f], Várt: %.2f, Kimenet: %.4f\n",
               inputs[sample][0], inputs[sample][1], expected_outputs[sample][0], output[0]);
    }

    // Tesztelés új bemenetekkel
    double test_inputs[3][INPUT_NODES] = {
        {0.4, 0.6},  // Átlag: 0.5
        {0.2, 0.8},  // Átlag: 0.5
        {0.9, 0.1}   // Átlag: 0.5
    };

    printf("\nTeszt kimenetek:\n");
    for (int i = 0; i < 3; i++) {
        forward_pass((double *)test_inputs[i], hidden_layer_output, output,
                     (double *)weights_input_to_hidden, (double *)weights_hidden_to_output);

        double expected = (test_inputs[i][0] + test_inputs[i][1]) / 2.0;  // A bemenetek átlaga
        printf("Bemenet: [%.2f, %.2f], Várt (átlag): %.2f, Kimenet: %.4f\n",
               test_inputs[i][0], test_inputs[i][1], expected, output[0]);
    }

    return 0;
}