A magyar nyelvben is ismert kalkulál, kalkulátor szó eredete a latin calculus. Jelentése kavics, kis kő. Gondoljunk bele, elszámolni 762-ig mekkora munka lenne. De - ha a tízes számrendszerben gondolkodva - az egyeseket kis kövek, a tízeseket nagyobb kövek, a százasokat még nagyobb kövek reprezentálják, akkor ezzel az absztrakcióval a számítási módszer leegyszerűsödhet.

Nem tudni pontosan, mikor kezdték el használni az első számolásra tervezett eszközt, az abakuszt. Az elfogadott elméletek szerint története időszámításunk előtt 2400-ban Babilóniában kezdődött. Maga az abakusz szó görög eredetű, tábla vagy asztal jelentéssel bírt.

Az fennmaradt első írásos emlék az abakuszról Heródes írása, aki egy abakuszt használó öreg egyiptomiról ír. Salamis szigetén találták meg a jelenleg ismert legrégebbi abakuszt.

Egy rekonstruált, valószínűleg a római korból származó abakuszt mutat a következő ábra. Ez néhány csúszkát vagy szánt tartalmaz, amelyek mindegyikén meghatározott számú, esetleg más-más színű, elcsúsztatható golyó vagy korong található.

Játék: végezze az alábbi linken lévő feladatokat:

John Napier skót tudós számos matematikai módszert dolgozott ki, amelyeket 1617-ben bekövetkezett halála után publikáltak. Belefáradván a nagy számok összeszorzásába, a legnagyobb elismerést a Napier pálcikák néven ismert szorzó masinája alkotta.

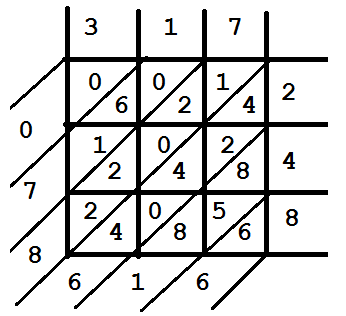
A példa a 317⋅248 szorzat kiszámításának lépéseit adja meg:

A felső sorba a szorzandót, a jobb oldali oszlopba a szorzót írtam. Mindkettő háromjegyű szám, így középen egy 3×3 mátrix van. Ezekben az adott sor és oszlop számjegyeinek szorzata van, jobb lent az egyesek, bal fent a tízesek.

A jobb alsó sarokban kezdve a diagonális sávok összegét kiszámolom, szükség esetén átviszem a tízeseket a következő diagonális sávba.

Így 317⋅248=078616 lesz az eredmény

Napier készített 10 csíkot a 10 számjegynek és előre felírta az adott számjegy szorzótábláját.

Egymás mellé rakta a pálcikákat és a jobb oldalt kiválasztott számjeggyel már lehet is szorozni. A módszert továbbfejlesztve elérte, hogy olyan számokat is összeszorozhasson, amelyben ismétlődnek a számjegyek.

A logarléc egy mechanikus analóg számológép. A logarléc feltalálását 1620-1630 időszakra datálják, miután John Napier publikálta a logaritmus fogalmát.

A szorzás, osztás műveletein kívül a kivonást, a logaritmust és a trigonometrikus függvényeket is támogatja.

A szorzást a logaritmikus azonosságokon keresztül támogatja:

$$ log(x \cdot y) = log(x) + log (y) $$

Számoljuk ki a 3*2 értéket. Ehhez a felső logarlécet eltoljuk az alsón úgy, hogy a skála a 2 értéknél kezdődjön. Levetítjük a felső lécen a 3 értékét az alsóra. 6-ot kapunk, ez a szorzat.

Az osztásra vonatkozóan nézzük az \(5.5 : 2\) példát.

Az alsó léc 5,5 értékéhez illesszük a felső léc 2 értékét. A felső léc skálájának kezdetén leolvashatjuk az eredményt, ami 2,75.

Charles Babbage angol matematikus és tudós tekinthető az első programozható számítógép feltalálójának. Sajnos, a megvalósítás terheit nem vállalta fel, ezért saját maga működő számítógépét nem láthatta.

A tervei és fennmaradt alkatrészek alapján később rekonstruálták a találmányait. Két gépet is tervezett, amelyet számon tart az utókor: az analytical engine és a differential engine nevűt. Az előbbi polinomtáblákat tartalmazott, így reprezentálta a számokat. Az utóbbi géphez lyukkártyás beolvasót és nyomtatót tervezett.

A számítógépének jól definiált architektúrája volt. A memória nagyon hasonlatos egy mai számítógép memóriájához, azzal a különbséggel, hogy fémből készült, fogaskerekek kötegeiből, 30 fogaskerék magasságban. Képzelj el egy magas, száz meg száz fogaskerékből álló tornyot, amelyek mindegyikén számok vannak. Ez egy decimális gép. Minden műveletet decimális alapon végez. Ő azonban már gondolt a bináris változatra is. A probléma a binárissal azonban az, hogy a gép már túl magas lett volna.

Volt benne CPU. A CPU képes volt elvégezni a négy aritmetikai alapműveletet – összeadást, szorzást, kivonást, osztást – már ezt is egy bravúr megvalósítani fémből. Egyúttal tudott valami olyat, amit egy számítógép tud, egy számológép viszont nem. Ez a gép képes volt saját memóriáját olvasni és döntést hozni. Ismerte az “if then” programozási alapműveletet, és ettől alapvetően számítógéppé vált. Számítógépként működött, nem csupán számológépként. Annál sokkal többet tudott,

Ada Lovelace volt az, aki megértette Babbage gépének a zsenialitását, és programot írt hozzá. Manapság sokan őt tartják az első programozónak. Bár történetileg nézve nem teljesen helytálló, hogy ő az első programozó, valójában egy ennél sokkal lenyűgözőbb dolgot hajtott végre. Ahelyett, hogy egyszerűen programozó lett volna, felismert valamit, amit Babbage nem.

Babbage megszállottja volt a matematikának. Egy matematikai célú gépezetet készített, amire Lovelace azt mondta: “Ez a gépezet matematikai feladványok megoldásánál sokkal többre képes.”. Ha közelebbről megnézzük, egy telefon, egy számítógép vagy bármely más számítógépes eszköz elemeit, akkor matematikát találunk. Végső soron minden a számokra épül. Legyen az videó, szöveg, zene vagy hang, mindennek az alapjai a számok, matematikai függvények, és Lovelace azt mondta: “Az, hogy matematikai függvényekkel és szimbólumokkal foglalkozunk, nem jelenti azt, hogy ezek a dolgok nem jelenthetnek más valós dolgokat, mint például zenét.”