Definíció szerint: „tudományon a természet, a társadalom és a gondolkodás objektív összefüggéseiről szerzett, igazolható ismeretek rendszerét értjük”. Más megfogalmazás szerint a tudomány elsősorban azokkal a dolgokkal foglalkozik, amelyek az öt érzékszervünkkel megfigyelhetők vagy megmérhetők. A tudomány arra törekszik, hogy folyamatosan gyűjtse és magyarázatokat adjon azokra a tényekre, amelyek a minket körülvevő környezetből, az univerzumból származnak.

A történelmileg létrejött társadalmi tudatformák közül a következő sajátos tulajdonságok emelik ki a tudományokat:

(1) rendelkeznek olyan, nagyhorderejű fogalmakkal és logikai eszközökkel, amelyekkel széles, általános vagy egyetemes érvényű elveket, törvényeket fogalmaznak meg;

(2) rendezetten írják le azokat az objektív feltételeket, amelyek között az elvek vagy törvények igazoltan, illetve bizonyítottan érvényesülnek.

(3) rendelkeznek olyan gondolati eszközökkel és módszerekkel, amelyekkel az ismert törvények alapján, adott feltételek között lehetséges vagy várható eredmények tényszerűen előre láthatók, illetve megvalósíthatóan tervezhetők;

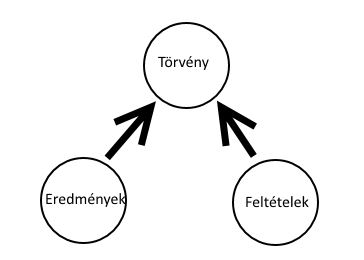
Törvények, a feltételek és az eredmények - e három kritérium alapján bármelyik tudományos problémát besorolhatjuk az alábbi problémacsoport valamelyikébe.

Indukció: ismertek a tárgyi feltételek, valamint a megvalósult eredmények és keressük az általános törvényt. Ez a klasszikus kísérleti fizika feladattípusa.

Magyarázat:

Az indukció valószínűleg a legfontosabb logikai módszer, amelyet a tudósok a törvények és elméletek megfogalmazásában használnak. Az indukció egy általánosító módszer, amelynek segítségével egy véges adathalmazból rögzített feltételek között egy egyetemes vagy általános állításra következtetünk (híres példa az indukció használatára a tudományban a Mendel féle öröklődési törvények felismerése és levezetése). Az indukció legnagyobb problémája annak igazolása, hogy kellő számú megfigyelést végeztünk-e ahhoz, hogy általános következtetést vonjunk le véges számú megfigyelésből.

A természettudományokban ugyanis mindig nem teljes indukcióról van szó. Minél nagyobb számú kísérletet hajtunk végre és az működik, az összefüggés felismerésében való bizalmunk egyre növekszik. Bizalmunk alapja az a feltevés, hogy a természet egységesen viselkedik. A matematikában használatos egzakt módszer, a teljes indukció esetében ilyen probléma nem merül fel.

Érdekesség: a jogtudomány vagy közelebbről a törvényhozási folyamat is az induktív módszerre épít, hiszen megfigyeli társadalmi problémákat, azok egyes eseteit, meghatározza a kiváltó feltételeket és és végeredményként törvényeket hoz.

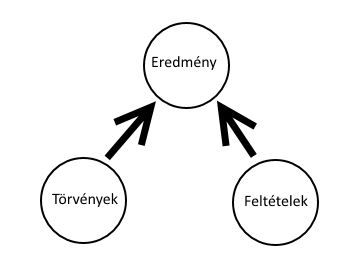
Dedukció: ismertek az általános törvények és a tárgyi feltételek és keressük a várható eredményt. Ez például az elméleti fizika tipikus feladata.

Magyarázat:

A deduktív következtetésnek központi szerepe van a tiszta matematikában, ahol az elméleteket úgy építik fel, hogy explicit módon megadott axiómákból deduktív következtetéseket vonnak le (mint az euklidészi geometriában). Az eredményeket (a matematikai tételeket) igaznak tekintik, ha van egy logikailag érvényes következtetési lánc, amely az axiómákból vezeti le őket. Az ilyen deduktív bizonyítások olyan bizonyossággal szolgálnak (feltéve, hogy az axiómák ellentmondásmentesek), amely az induktív tudományokban elérhetetlen. A deduktív logika azonban nem tudja megerősíteni az eljárásban szereplő egyetlen állítás igaz voltát sem. A logika mindössze annyit mondhat nekünk, hogy ha a premisszák igazak, és az érvelés logikailag helyes, akkor a konklúzió is igaz.

Érdekesség: Bolyai János, magyar matematikus édesapjának írja egyik levelében: „Semmiből egy új, más világot teremtettem”. Teszi ezt azért, mert rájött, ha az Euklideszi törvények közül egyet megváltoztat, akkor akár egy új (ma azt mondanánk, virtuális) világ is keletkezhet képzeletben. Saját korában még rácsodálkoztak arra, hogy ilyen világ csak a képzeletünkben létezik. De a 20. századi tudomány bizonyította, hogy valójában a mai világuk pontosan egy ilyen nem Euklideszi törvényeken alapuló világ.

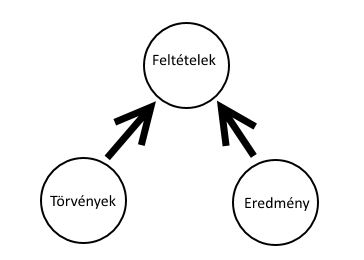
Redukció: ismeretesek az általános törvények, valamit a célul kitűzött eredmények és keressük azokat az objektív feltételeket, amelyek között a célok megvalósulhatnak.

Magyarázat:

Az ilyen típusú feladatok a műszaki tudományokra jellemzőek. A megoldás azonban a természettörvények alapján már nem invertálható egyértelműen, vagyis végtelen nagy lehet azon feltételrendszereknek a száma, amelyek a törvény hatálya alá esnek és szolgáltatják a célul kitűzött eredményeket. Ilyenkor meg kell elégednünk néhány (gyakran egyetlen) megoldással, amelyhez heurisztikus módon jutottunk el.

A redukció egy másik értelmezésével az elemi tudományos problémák osztályozásakor találkoztunk (A tudományok „háromsága”.) Itt a szóba jöhető megoldások számának ésszerű redukálása (csökkentése) a cél.