Az egyenlő valószínűségű, teljesen rendezetlen eseményhalmazról szóló hírkészlet átlagos információtartalma a legnagyobb. A teljesen rendezett, azaz előre ismert eseményhalmazról szóló hírkészlet átlagos információtartalma a legkisebb.

A hírkészlet valószínűségi eloszlása az átlagos információtartalmat, azaz az entrópiát elmozdítja a lehetséges maximumtól. Az ilyen hírkészlet redundáns.

A redundancia azt fejezi ki tehát, hogy milyen mértékben tér el az eseményrendszer átlagos információtartalma a maximálistól.

A redundancia mértéke:

$$ R = \frac{H_{max} -H}{H_{max}} = 1- \frac{H}{H_{max}} $$

Ha az eseménytér n egyenlő valószínűségű eseményből áll:

$$ H_{max} = log_2 n \, \,{és}\,\, R = 1- \frac{H(p_1, ... , p_n)}{log_2 n}$$

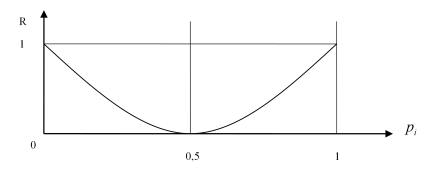
A redundancia nem feltétlenül negatív tulajdonság, pl. a hírközléselméletben is jelentős szerepet játszik. A redundancia teszi lehetővé a hírek biztonságos kommunikációját zajos csatornán. Az ember szóbeli kommunikációjának redundanciája átlagosan több mint 30%. A kéteseményes hírkészlet redundanciájának változását az alábbi ábra szemlélteti:

Tehát a redundancia akkor minimális, ha az események valószínűsége egyforma.

Az entrópiánál bemutatott példa folytatásaként számoljuk ki az ott bemutatott rendszer redundanciáját.

Számoljuk ki mekkora a maximális entrópia?

$$ H_{max} = log_2 n = log_2 4 = 2 $$

Ekkor a redundancia képletébe behelyettesítve:

$$ R = 1- \frac{H}{H_{max}}=1-\frac{1.68}{2} = 0.16 $$,

azaz az eseményrendszer redundanciája ~16%.