Table of Contents
Adattömörítő eljárások
A tömörítő eljárások lényege: olyan változó szóhosszúságú kódot választunk, hogy a sokszor előforduló szimbólumokhoz rövidebb, míg a ritkábbakhoz hosszabb kódot rendelünk.
Shannon-Fano eljárás
Egyszerű adattömörítési eljárás, amelynek lényege az, hogy:
- A továbbítandó szimbólumokat valószínűség szerint rendezzük.
- A szimbólumhalmaz két lehetőség azonos valószínűségű részhalmazra bontjuk. Az egyikhez 0, a másikhoz 1 szimbólummal kezdődő szót rendelünk.
- Az eljárást addig folytatjuk, míg el nem fogynak szimbólumok.
Példa
| Szimbólum | Valószínűség | Kód | Szóhossz |
|---|---|---|---|
| X1 | 0.25 | 00 | 2 |
| X2 | 0.25 | 01 | 2 |
| X3 | 0.125 | 100 | 3 |
| X4 | 0.125 | 101 | 3 |
| X5 | 0.0625 | 1100 | 4 |
| X6 | 0.0625 | 1101 | 4 |
| X7 | 0.0625 | 1110 | 4 |
| X8 | 0.0625 | 1111 | 4 |
8 szimbólumot használunk a kódolásnál, amelynek egyes szimbólumai a táblázatban megadott valószínűséggel szerepelnek a küldendő üzenetben. Ezeket előfordulási gyakoriság alapján csökkenő sorrendbe rendeztük, azaz a leggyakoribbak vannak elől. A harmadik oszlopban hozzárendeltük változó hosszúságú kódokat, a gyakoriakhoz hosszabbakat.
A 8 szimbólum teljes eseményrendszert alkot, hiszen egymást kizáró eseményekből áll, valamint a szimbólumok előfordulási valószínűségeik összege 1.
Tömörítsük az X2 X3 X8 X7 X1 üzenetet:
Az eredmény:
011001111111000
A tömörítés nélkül az üzenet hossza 4 * 5 azaz 20 bit lett volna. A tömörítés után 15 bitre csökkent.
Számítsuk ki a kód entrópiáját.
$$ H = - (\frac{2}{4}log\frac{1}{4} + \frac{2}{8} log \frac{1}{8} + \frac{4}{16} log \frac{1}{16}) = 2.75 \,\, [bit]$$
Huffman kódolás
A Huffman kódolás egy veszteségmentes adatkompressziós algoritmus, amely a gyakrabban előforduló szimbólumokhoz rövidebb, míg a ritkábban előfordulókhoz hosszabb kódokat rendel. Ez az előfordulási gyakoriság alapján történik az adatban. Az eljárás optimális, mert a legkisebb átlagos kódhosszt eredményezi.
A Huffman-kódolás lépései
- Számoljuk ki az egyes karakterek előfordulási gyakoriságát az adatban.
- Építsünk bináris fát a gyakorisági adatok alapján.
- Rendeljünk bináris kódokat minden karakterhez a fa szerkezetét követve, biztosítva, hogy a gyakoribb karakterek rövidebb kódokat kapjanak.
Huffman-kódolási példa
Kódoljuk a következő szöveget: BACADAEAFABBAAAGAH
Gyakoriságok meghatározása
| Karakter | Gyakoriság |
|---|---|
| A | 9 |
| B | 3 |
| C | 1 |
| D | 1 |
| E | 1 |
| F | 1 |
| G | 1 |
| H | 1 |
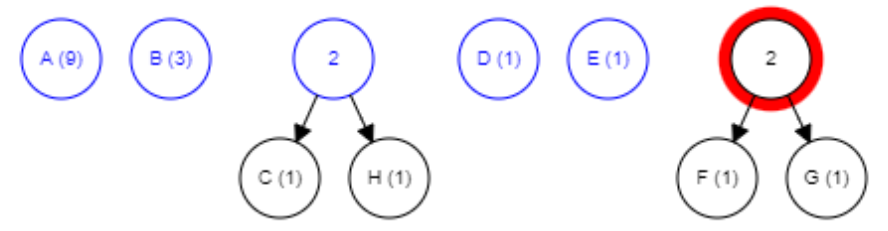
Készítsük el a bináris fa leveleit úgy, hogy zárójelben feltüntetjük a gyakoriságokat:
Válasszuk ki a két legkisebb gyakoriságú levelet és vonjuk össze az alábbiak szerint:
Vonjuk össze a F és G leveleket is ugyanígy:
Vonjuk össze a D és E leveleket is ugyanígy:
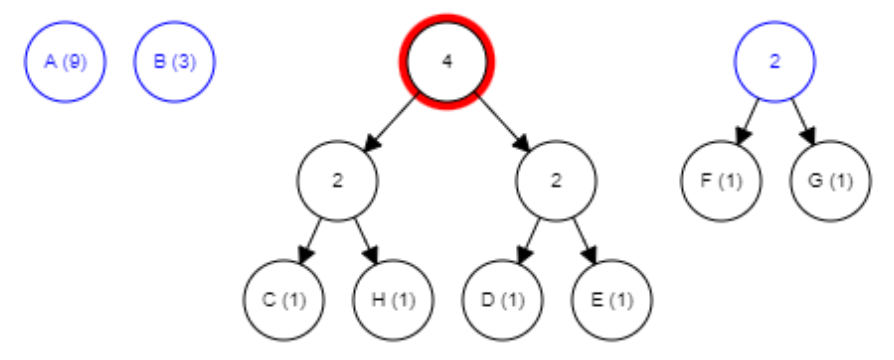
Most a középső két levél tartalmazza legkisebb gyakoriságot, ezért vonjuk őket össze:
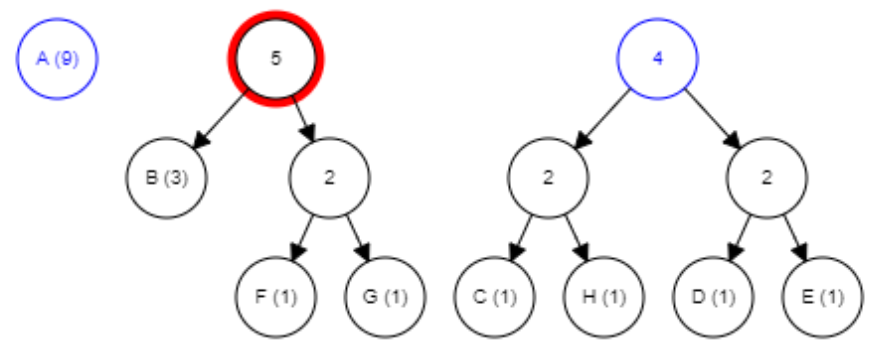
Most a B és a jobb oldali 2-vel jelölt levél tartalmazza legkisebb gyakoriságot, ezért ezeket vonjuk össze:
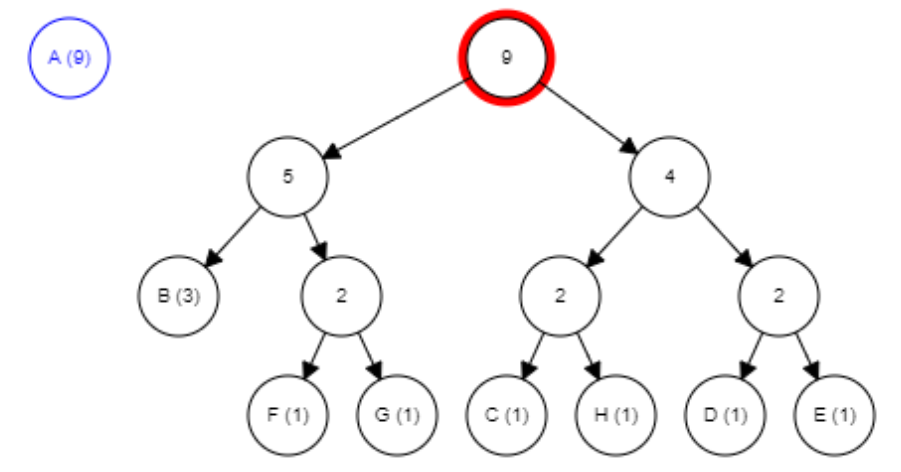
Most vonjuk össze az utolsó két megmaradt levelet:
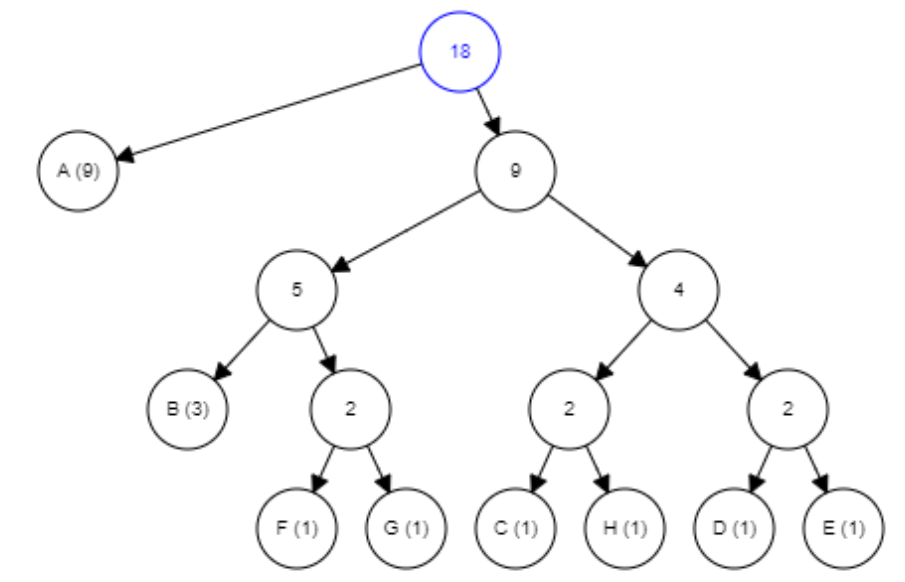
A végén ez a fa lesz az eredmény:
Bináris kód hozzárendelés a fa leveleihez
A bináris fa létrehozása után, rendeljük a levelekhez a kódokat, felülről lefelé haladva balra mozdulva 0-val, jobbra mozdulva 1-el egészítjük ki a kódot.
| Karakter | Bináris kód |
|---|---|
| A | 0 |
| B | 100 |
| C | 1100 |
| D | 1110 |
| E | 1111 |
| F | 1010 |
| G | 1011 |
| H | 1101 |
Az eredmény a következő lesz:
BACADAEAFABBAAAGAH -> 100|0|1100|0|1110|0|....|1101
Hasonló módon készül el a végleges kód, mint a Shannon-Fano kódolás esetén, csak itt a fa készítés segít a bináris hozzárendelés elkészítésében.
megjegyzés: a | karakter természetesen nincs benne az eredményben, itt csak az átláthatóság miatt szerepel, ebben a módszerben sincs és nem is kell elválasztó jelzés.
LZW kódolás
Ennél a módszernél, nem kell tudni a forrásadatokban szereplő szimbólum gyakoriságokat. Menet közben gyűjtünk információt a forrásszimbólumokról. Az LZW kódolás az úgynevezett adaptív kódok csoportjába tartozik.
Algoritmusa
Kiindulásként a kódtáblázat tartalmazza a forrás összes előforduló elemét. A kódoláskor az éppen aktuális pozíciótól kezdve addig olvassuk be a soron következő szimbólumokat egy bufferbe (b), amíg a sorozat szerepel a szótárban. Ha a soron következő karakter (c) az első olyan elem, amelyre bc már nem szerepel a szótárban, akkor b indexe lesz a soron következő kód a szótárban és a szótárt bc-vel bővítjük és c karaktertől folytatjuk a kódolást.
Ezt a tömör leírást egy példa alapján tesszük érthetővé.
Példa
Kódoljuk a következő sorozatot LZW kódolással:
dabbacdabbacdabbacdabbacdeecdeecdee
Megvizsgálva az adatforrást, látható hogy csak 5 különböző szimbólumból áll: (a,b,c,d,e). A szótárt kezdetben ezzel az 5 elemmel töltjük fel.
- A kódoló először d karaktert veszi.
- A d benne van a szótárban, így hozzáilleszti a következő, az a karaktert.
- A da már nem szerepel jelenleg a szótárban, ezért:
- d 4-es indexét lejegyzi
- felveszi a szótárba da részszöveget a 6. bejegyzésbe és megy tovább a-val folytatva.
- Az a szerepel a szótárban, ezért hozzáveszi a következő b elemet, és mivel ab nem szerepel a szótárban, így a indexét az 1-et lejegyzi, majd ab-t 7. elemként a szótárhoz illeszti az algoritmus. A kódolás végén a következő indexek jelennek meg:
4,1,2,2,1,3,6,8,10,12,9,11,7,16,4,5,5,11,21,23,5
| index | bejegyzés |
|---|---|
| 1 | a |
| 2 | b |
| 3 | c |
| 4 | d |
| 5 | e |
| 6 | da |
| 7 | ab |
| 8 | bb |
| 9 | ba |
| 10 | ac |
| 11 | cd |
| 12 | dab |
| 13 | bba |
| 14 | acd |
| 15 | dabb |
| 16 | bac |
| 17 | cda |
| 18 | abb |
| 19 | bacd |
| 20 | de |
| 21 | ee |
| 22 | ec |
| 23 | cde |
| 24 | eec |
| 25 | cdee |
A Unix compress parancsa és a GIF (Graphics Interchange Format) képtömörítő eljárás is az LZW algoritmust alkalmazza.
RLE kódolás
Run-Length Encoding (RLE) – futáshossz kódolás.
A fentiekhez képes nagyon egyszerű, de mégis a gyakorlatban széleskörben használt kódolás.
Egyszerű tömörítési eljárás, amely a hosszasan ismétlődő azonos karaktereket, biteket egyetlen szimbólummal és egy ismétlésszámmal kódolja. Fekete-fehér képek tömörítésére használták korábban, de a TGA, PCX formátumok, valamint a FAX gépek is használják, textúra tömörítéshez is jó lehet. Példa alapján könnyen érthető.
Kódoljuk a következő karaktereket RLE kódolással:
WWWWWWWWWWWWBWWWWWWWWWWWWBBBWWWWWWWWWWWWWWWWWWWWWWWWBWWWWWWWWWWWWWWW
Kódolva
12W1B12W3B24W1B14W
Melynek értelmezése: 12 darab W, 1 darab B, 12 darab W, 3 darab B, stb.
Így tehát a Run-Length Encodinggal kódolt szöveg az eredeti 67 karaktert 18-cal írja le. Természetesen a valóságban nem karakterekkel, hanem bináris kóddal használják.