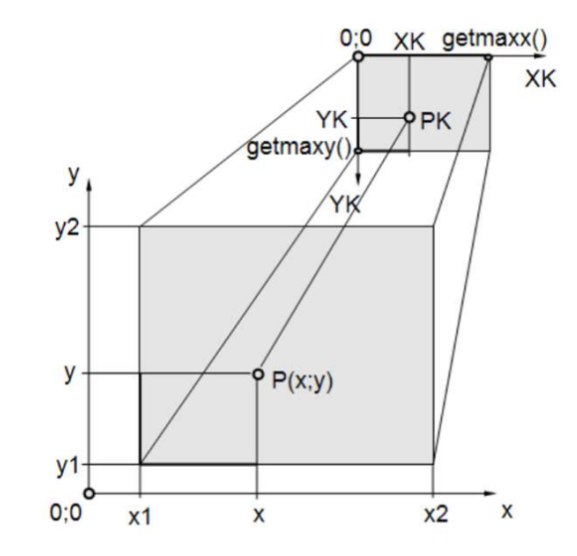
A következő ábrán látható a világ és a képernyő koordináta rendszer viszonya:

Feladatunk, hogy meghatározzuk a $P(x;y)$ pont helyzetét a képernyőn amit $PK(XK,YK)$-val jelölünk. A lenti nagyobb világkoordinátarendszer téglalap bal alsó sarka: $(x_1,y_1)$, a jobb felső sarka $(x_2,y_2)$. Tehát nem feltételül az origóból indul.

Viszont a fenti képernyő koordináta rendszer bal felső sarka mindig az origó lesz.

Először számoljuk ki a két szürke téglalapok oldalarányait:

A vízszintes arány: $L_x = getmaxx() / (x_2 - x_1)$ lesz.

A függőleges arány: $L_y = getmaxy() / (y_2 - y_1)$ lesz.

Tehát a képernyőt jelképező kisebb téglalap oldalainak mérete: $getmaxx()$ és $getmaxy()$

A leképezésben az $XK$, azaz a pont képének $x$ koordinátája az alábbi szorzattal fejezhető ki:

$XK = L_x (x - x_1)$

Az KY koordináta is hasonlóan $L_y (y - y_1)$ lenne, de a képernyőn a $y$ irány fordítva van, felülről lefelé növekszik, azért a képlet:

$YK = getmaxy() - L_y (y - y_1)$

Mivel a getmaxy() az oldalarány képletből felírható: $getmaxy() = L_y (y_2 - y_1)$, ezért behelyettesítés után:

$YK = L_y (y_2 - y_1) - L_y (y - y_1) = L_y y_2 - L_y y_1 - L_y y + L_y y_1$

$L_y * y_1$ kiesik az egyszerűsítés után, mert plusz és mínusz előjellel is szerepelnek.

$YK = L_y y_2 - L_y y = L_y * (y_2 - y)$

Tehát összegezve:

$XK = L_x (x - x_1)$

$YK = L_y (y_2 - y)$