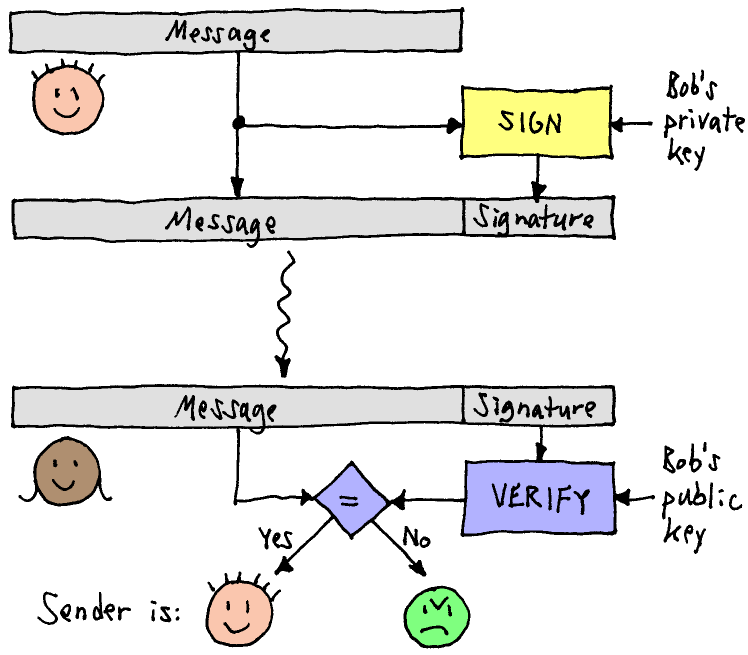
Digital Signature Using Hash Functions
A hash function acts like a digital fingerprint for a document. The function ensures that the hash code is varied enough for any given document. But how does digital signing work with this process?
Steps:
1. Compute the hash: Calculate \( y = H(x) \) for a document \( x \). This creates a unique “fingerprint” of the document.
2. Encrypt the hash: Use the private key to encrypt the hash \( y \).
3. Attach the result: The encrypted hash is attached to the document as the signature.
Consequences
- The signed document remains readable.
- The signature can be stored separately from the document, for example, at a notary or in a database.
During network communication, the following data is transmitted:
1. The original document.
2. The hash of the document, encrypted with the sender's private key.
3. The sender’s public key.
How to Verify the Integrity of the Signature
1. Calculate the hash of the received document.
2. Decrypt the encrypted hash using the sender’s public key.
3. Compare the two hash codes. If they match, the document's integrity is intact.
This process ensures that the document has not been tampered with and that the signature is valid.