Huffman codes
Huffman encoding is a lossless data compression algorithm that compresses data by assigning shorter codes to more frequent symbols and longer codes to less frequent ones. It is based on the frequency of a symbol's occurrence in the input data. This method is optimal because it produces the smallest possible average code length.
Steps in Huffman Encoding
- Calculate the frequency of each character in the input data.
- Build a binary tree from the frequency data.
- Assign binary codes to each character based on the tree's structure, ensuring that more frequent characters get shorter codes.
Example of Huffman Encoding
Let’s walk through an example step-by-step:
Step 1: Calculate Frequency
Suppose we want to encode the following string:
BACADAEAFABBAAAGAH
First, calculate the frequency of each character in the string:
| Character | Frequency |
|---|---|
| A | 7 |
| B | 3 |
| C | 1 |
| D | 1 |
| E | 1 |
| F | 1 |
| G | 2 |
| H | 1 |
Step 2: Build the Huffman Tree
1.) Create a leaf node for each character and its frequency.
2.) Merge the two nodes with the lowest frequency. Create a new node with these two nodes as children, and the frequency of the new node is the sum of the two children's frequencies. Repeat this process until only one node (the root) remains.
Start with the frequencies:
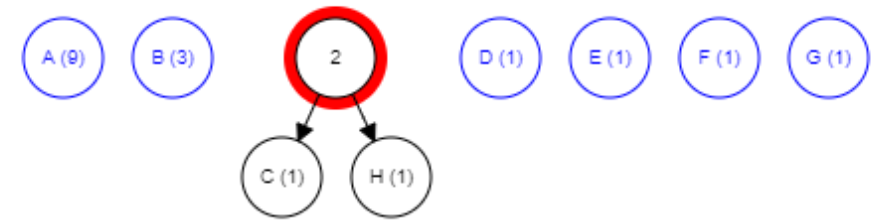
First, combine the two lowest frequency nodes. Let’s combine C and H (both have frequency 1):
Combine the two lowest frequency nodes: F and G
Combine the two lowest frequency nodes: D and E
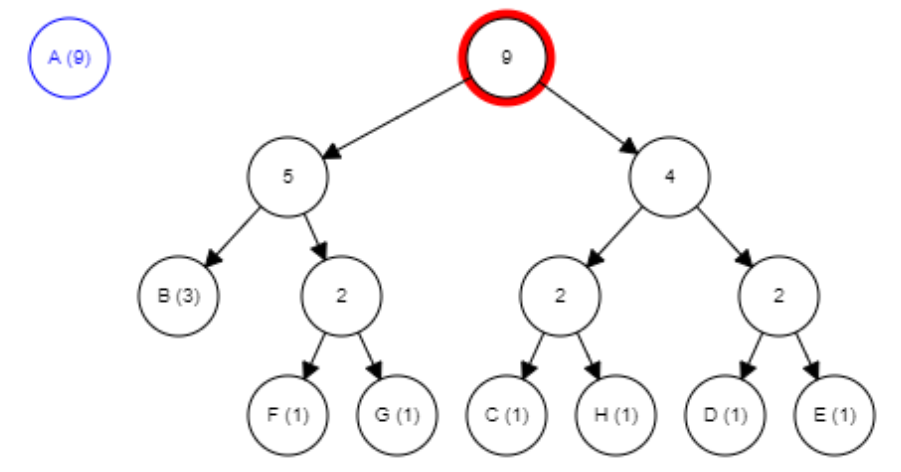
Merging two nodes with lowest frequency:
Merging two nodes with lowest frequency
Merging two nodes with lowest frequency
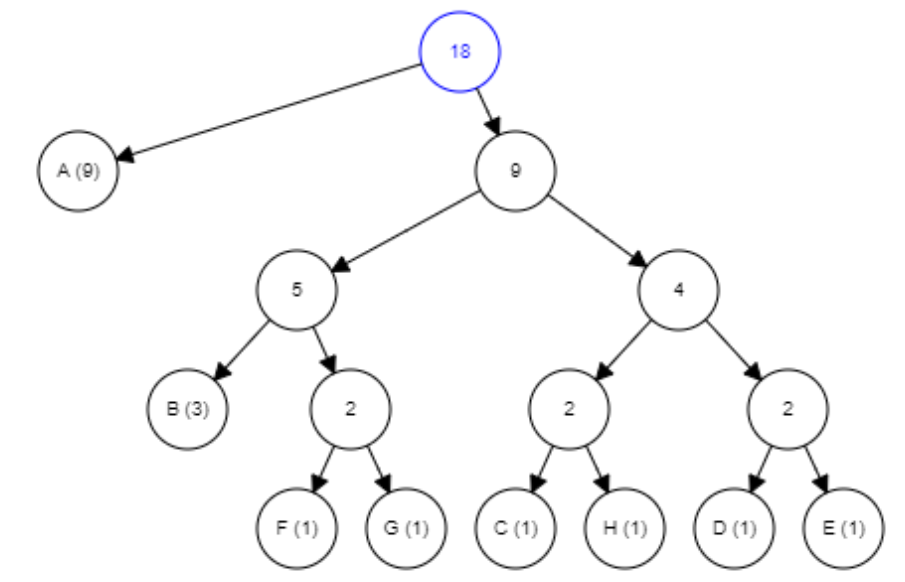
Final tree:
Step 3: Assign Binary Codes
After building the tree, assign binary codes to each character by traversing the tree. Typically, moving left adds a 0, and moving right adds a 1.
| Character | Binary Code |
|---|---|
| A | 0 |
| B | 100 |
| C | 1100 |
| D | 1110 |
| E | 1111 |
| F | 1010 |
| G | 1011 |
| H | 1101 |
Huffman encoded result:
BACADAEAFABBAAAGAH -> 100|0|1100|0|1110|0|....|1101