Experience shows that the information value of certain news depends on their probability.

$$ I_{E_i} = f(P_i) $$

in which \( I_{E_i} \) means the information value. In this aspect the more unexpected or unlikely (rumour) a news is the bigger it's news value.

So the \(f\) function was selected according to Shannon's suggestion:

$$ I_E = \log_2 \frac{1}{p_E} = -\log_2( p_E ) [bit] $$

The properties of a logarithm function play an important role in the modeling procedure of the quantitative properties of a given information.

If an event space consist of two equal-probability event \(p(E_1) = p(E_2) = 0.5 \) then,

$$ I_{E_1} = I_{E_2} = \log_2 \frac{1}{0.5} = - \log_2 0.5 = 1 [bit] $$

So the unit of the information means the news value which is connected to the simple, less likely, same probability choice.

If the event system consist of n number of events and all these events have the same probability then the probability of any event is the following:

$$ p_E = \frac{1}{n} $$

In these cases, the news value which is connected to these events will be the following:

$$ I_E = \log_2 \frac{1}{p_E} = \log_2 (n) [bit] $$

If the events in the event space are not equally likely, then the set of messages can be well characterized by the average information content of the messages.

The average information content of the set of messages is called the entropy of the message set.

$$ H_E = \sum_{i=1}^n p_i \cdot I_{E_i} = \sum_{i=1}^n p_i \cdot \log_2 \frac{1}{p_i} = - \sum_{i=1}^n p_i \cdot \log_2 p_i$$

Example: Given an event space consisting of two events: \( E = \{E_1, E_2\} \), and further \( p = \{p_1, p_2\} \) with \( p_2 = 1 - p_1 \), then the average information content is:

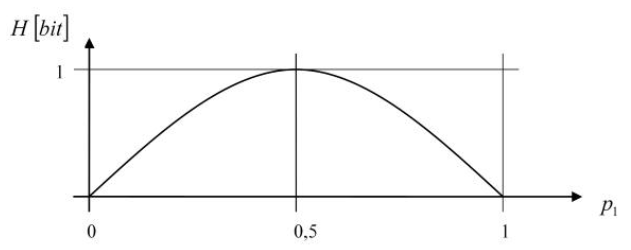
$$ H_E = -[p_1 \cdot \log p_1 + (1 - p_1) \cdot \log (1 - p_1) ] $$

This function can be represented as follows:

We can see that entropy is highest when the two events are equally likely. In general, in this model, entropy is low when our event system includes events with low probabilities.

Entropy can also be viewed as a measure of the information “richness” of a message. In communication systems, higher entropy implies a greater potential for the message to carry a variety of content, whereas lower entropy suggests that the message is more predictable or redundant.

This concept is crucial in various fields, including data compression, cryptography, and machine learning, where understanding and managing entropy can lead to more efficient algorithms and systems. For example, in data compression, reducing redundancy (and thus reducing entropy) can lead to more compact data representations. Similarly, in cryptography, managing entropy ensures that keys and encrypted messages are less predictable and more secure.

The average information content of a message set describing an equally probable, completely random set of events is the highest. In contrast, the average information content of a message set describing a completely ordered, i.e., fully known event set, is the lowest.

A probability distribution that deviates from the maximum possible entropy leads to a message set that is redundant.

The measure of redundancy is:

$$ R = \frac{H_{max} - H}{H_{max}} = 1- \frac{H}{H_{max}} $$

If the event space consists of n equally probable events:

$$ H_{max} = \log_2 n \;\; \text{and} \;\; R = 1 - \frac{H(p_1, ... , p_n)}{\log_2 n} $$

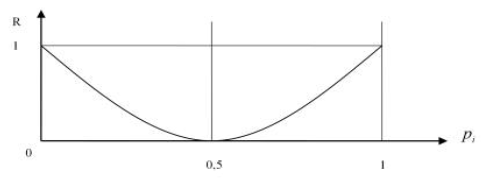
Redundancy plays a significant role in information theory. Redundancy enables the secure communication of messages over a noisy channel. The redundancy of human verbal communication is typically more than 30%. The changes in redundancy for a two-event message set are illustrated in the figure below:

Thus, redundancy is minimal when the probabilities of the events are equal.

Example: The occurrence probabilities of a system consisting of four events are as follows:

$$ E = \{E_1, E_2, E_3, E_4 \}, $$

and the probabilities of the individual events are as follows:

$$ p = \{0.5, 0.25, 0.2, 0.05\}. $$

The individual information content for the states of the system are:

$$ I_{E_1} = -\log_2 0.5 = 1 \, \text{[bit]}, $$ $$ I_{E_2} = -\log_2 0.25 = 2 \, \text{[bit]}, $$ $$ I_{E_3} = -\log_2 0.2 = 2.32 \, \text{[bit]}, $$ $$ I_{E_4} = -\log_2 0.05 = 4.32 \, \text{[bit]}, $$

What is the entropy of the message set?

$$ H_E = \sum_{i=1}^{4} p_i \cdot I_{E_i} = 0.5 \cdot 1 + 0.25 \cdot 2 + 0.2 \cdot 2.32 + 0.05 \cdot 4.32 = 1.68 \, \text{[bit]}. $$

What is the redundancy of the message set?

Let's calculate the maximum entropy:

$$ H_{\text{max}} = \log_2 n = \log_2 4 = 2 [bit]$$

Then, substituting into the formula for redundancy:

$$ R = 1 - \frac{H}{H_{\text{max}}} = 1 - \frac{1.68}{2} = 0.16, $$

which means the redundancy of the event system is approximately 16%.

Why do not store raw password strings in compiled code?

#include <stdio.h>
#include <math.h>

float calculateEntropy(unsigned int bytes[], int length);

char sample[] = "Some poetry types are unique to particular cultures and  genres and respond to yQ%v?FY}ZT=/5cJ.m~A{9^8Lse characteristics of the language in which the poet writes. Readers accustomed to identifying poetry with Dante, Goethe, Mickiewicz, or Rumi may think of it as written in lines based on rhyme and regular meter. There are, however, traditions, such as Biblical poetry and alliterative verse, that use other means to create rhythm and euphony. Much modern poetry reflects a critique of poetic tradition,[6] testing the principle of euphony itself or altogether forgoing rhyme or set rhythm";

int main()
{
    unsigned int byteCounter[256];
    const int windowWidth = 20;

    for(int i = 0; i < sizeof(sample) - windowWidth; i++)
    {
        memset(byteCounter, 0, sizeof(unsigned int) * 256);

        char *p = &sample[i];
        char *end = &sample[i + windowWidth];

        while(p != end)
        {
            byteCounter[(unsigned char)(*p++)]++;
        }
        float entropy = calculateEntropy(byteCounter, windowWidth);
        printf("%d - %.3f\n", i, entropy);
    }


}


float calculateEntropy(unsigned int bytes[], int length)
{
    float entropy = 0.0f;

    for (int i = 0; i < 256; i++)
    {
        if (bytes[i] != 0)
        {
            float freq = (float) bytes[i] / (float) length;
            entropy += -freq * log2f(freq);
        }
    }
    return entropy;
}