A relation can be narrowly defined as a tool for establishing a connection between two sets. Let \( A \) and \( B \) be two sets. The relation \( R \) creates a connection between these two sets. Let:

\[ C = A \times B = \{(a, b) \mid a \in A, b \in B\} \]

Here, \( C \) is the Cartesian product of sets \( A \) and \( B \). The elements of set \( C \) are ordered pairs from \( A \) and \( B \). The relation \( R \) itself is a set, which is a subset of \( C \).

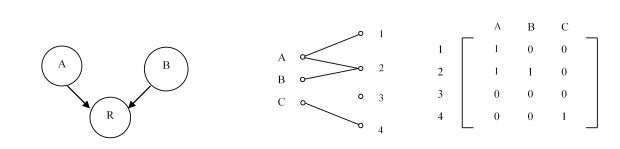
For example, the relation describing the connection between sets \( A \) and \( B \), or the connection between \( A, B, C \to 1, 2, 3, 4 \), can be represented using a graph or a matrix.

The relation between the sets \( A, B, C \) and \( 1, 2, 3, 4 \) is shown in the middle diagram. This relationship can also be written using a matrix, as shown in the third diagram. Note that there are 1's where the row and column sets are related. The set without a connection will have only 0's in its row.

Important!

A relation is homogeneous if it is defined on a single set. Relations are generally binary, which means that the relation set contains pairs of two elements. Relations are often expressed in the form of statements. For example, “Peter and Irma are married.”

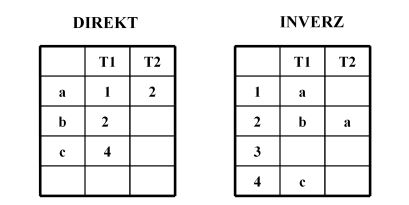
A relation can also have an inverse. The following diagram shows how a direct relationship can be transformed into its inverse: