Statistical properties

The outcome of experiments, the results of observations and the status of systems form a so-called 'event space', where finite or infinite cardinality elementary events may occur. In probability theory, an event space encompasses (includes) all possible outcomes of an experiment, such as flipping a coin, rolling a dice, or measuring the temperature of a system.

These events may form sets. Because they can be sets, we may perform standard set operations (union, intersection, complements, etc.) on them. For example, the union of two events in an experiment may represent the occurrence of either event, while the intersection represents the simultaneous occurrence of both. When these operations occur, the event will carry information.

The value of information related to these events can vary significantly based on everyday experience. For instance, knowing that a rare event has occurred (such as a lottery win) typically provides more valuable information than learning about an event that occurs frequently or predictably.

For example, if someone tells me that five of his numbers were drawn in the lottery, that information would be much more valuable than if they said only one number was drawn.

As we observe the outcomes of these events over time, we may conclude that certain events exhibit stability in their frequency of occurrence. For example, when repeatedly flipping a coin, we expect the event of landing heads to occur approximately 50% of the time, given enough trials. This regularity in frequency forms the basis for probability theory, where events with stable frequencies are described as having predictable probabilities.

In the \( E_i \) event space, an event happened \(k_i\) times then the frequency of that given event may be calculated with the following formula:

\(freq_i=\frac{k_i}{k} \)

This means that we divide the number of all events by the number (frequency) of that given event. In case of a large number of experiments this number will show us the probability of that event.

$$ \lim_{k \to \infty} freq_i = \frac{k_i}{k} = P(E_i) $$

• if \(k_i = k \), then the occurrence will be certain \(P(E) = 1 \)

• if \(k_i = 0 \), then the occurrence will be impossible \(P(E) = 0 \)

The event's \(𝐸\) probability \(p(E)\) will be the occurrence's probability.

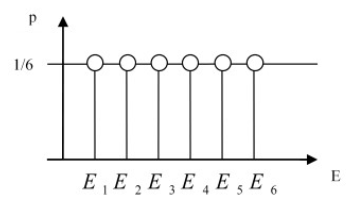
If we take the six-sided dice for our probability test the following will occur:

The probability of every event will be 1/6 which can be calculated with the following formula. The rolls (of the dice) will form a so-called full event system. In the case of a full event system the sum of the probabilities (of each event) is 1 (by definition).

If one of the events happens then the others can not happen:

$$ \sum_{i=1}^{n} p(E_i) = 1 \text{ where } E_i \cap E_j = 0 \text{ and } i \not = j $$

This formula applies to a set of mutually exclusive events. Since these events are disjoint (no overlap between any two different events) and they together cover all possible outcomes (the sum of their probabilities is 1).

What is the sum of two different events' probability?

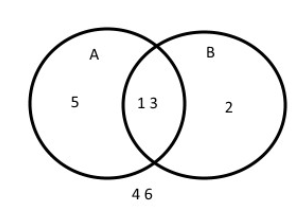
Example 1: what is the probability that we roll an odd number (with a dice) (Event A) and a number less then 4 (Event B)?

If A and B event would not have common events (so that they would exclude each other) the formula would be the following: \( p(A \cup B) = p(A) + p(B) \).

We can only form a general formula, if we extract the probability of the intersection of both sets from the total sum:

$$ p(A \cup B) = p(A) + p(B) - p(A \cap B) $$

So we can say that (according to this formula) the total probability for both events is 4/6.

Example 2: What is the probability that we roll the dice twice and the results will be 6 in both cases?

The probability of throwing a 6 is 1/6, but we cannot multiply it by 2 and take the result (2/6). We can not do that because both events are independent. There is no connection between the 2 trials, so we have to look at them as independent events. So the result will be the multiplication of both events:

$$ p(A) \times p(B) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36} $$

Example 3: What is the probability of getting at least one 5 when rolling two dice?

Let Event A represent rolling a 5 on the first die and Event B represent rolling a 5 on the second die. These are independent events.

• The probability of rolling a 5 on the first die is: \( p(A) = \frac{1}{6} \)
• The probability of rolling a 5 on the second die is \( p(B) = \frac{1}{6} \)
• The probability of both dice showing a 5 (i.e, \( A \cap B \) is \( p(A \cap B) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36} \)

$$ p(A \cup B) = p(A) + p(B) - p(A \cap B) $$ $$ p(A \cup B) = \frac{1}{6} + \frac{1}{6} - \frac{1}{36} = \frac{2}{6} - \frac{1}{36} = \frac{12}{36} - \frac{1}{36} = \frac{11}{36} $$

Example 4:: Woman is expecting twins, what is the probability that one of the children will be a girl?

Create sets containing all the possibilities.

Try the following c code here: https://www.onlinegdb.com/online_c_compiler and examine the results.

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define SIMULATIONS 1000

// Function to simulate the birth of twins
int simulate_twins() {
    // Randomly determine the gender of the twins (0 = boy, 1 = girl)
    int first_child = rand() % 2;
    int second_child = rand() % 2;

    // Return 1 if there is at least one girl, otherwise 0
    return (first_child == 1 || second_child == 1);
}

int main() {
    int at_least_one_girl = 0;

    // Initialize the random number generator
    srand(time(0));

    // Simulate 1000 pairs of twins
    for (int i = 0; i < SIMULATIONS; i++) {
        if (simulate_twins()) {
            at_least_one_girl++;
        }
    }

    // Calculate and print the result
    double probability = (double)at_least_one_girl / SIMULATIONS * 100;
    printf("In %.2f%% of cases, there is at least one girl in the twin pair.\n", probability);

    return 0;
}

Example 5:: https://en.wikipedia.org/wiki/Monty_Hall_problem