Institute of Information Science - University of Miskolc

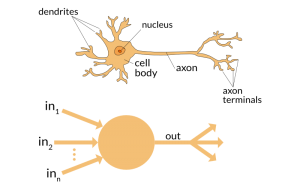
Az alábbi képen a biológiai neuront és annak mesterséges intelligencia modellekben használt analógját látjuk. A biológiai neuron az emberi agy alapvető építőeleme, amely információkat dolgoz fel és továbbít más neuronok felé. A neuron dendritekkel rendelkezik, amelyek a környező neuronoktól érkező jeleket fogadják. Ezeket a jeleket a sejt (amelyben a mag található) dolgozza fel, majd továbbküldi az axonon keresztül. Az axon végén található axon-végződések szinapszisokon keresztül kapcsolódnak más neuronokhoz, így biztosítva az információáramlást.

A mesterséges neuron, a fenti biológiai modell alapján működik, leegyszerűsítve annak alapvető működését. A mesterséges neuron bemeneteket fogad, amelyeket (matematikailag) súlyoz (ezzel vezérli a bemenet fontosságát), majd összegez. Az így kapott értéken egy aktivációs függvényt futtat, amely meghatározza, hogy a neuron “tüzel-e”, azaz továbbküldi-e a jelet. Az aktivációs függvény eredménye képezi a neuron kimenetét, amelyet továbbít a hálózat következő rétegeinek.

Az alábbi kép egy mesterséges neurális hálózat egyszerű modelljét ábrázolja.

A hálózat bemeneti réteggel indul, amely a zöld színű x₁ és x₂ elemeket tartalmazza. Ezek a bemeneti változók képviselik azokat az adatokat, amelyeket a modell feldolgoz. A bemeneteket súlyokkal szorozzák, majd átadják a rejtett rétegek neuronjaiba, amelyeket a kék színű z₁, z₂ és z₃ jelöl.

A rejtett réteg(ek)ben minden neuron kiszámítja a saját kimenetét egy aktivációs függvény segítségével, amely a bemeneti jelek összegét alakítja át (nemlineáris módon). Ezek a kimenetek aztán tovább haladnak a következő rétegekbe (a példában csak 1 rejtett réteget használunk, ezért itt nincs továbbadás), míg végül elérik a kimeneti réteget, amelyet itt az y_pred (y predikció) narancssárga elem jelöl.

Az y_pred a modell végső előrejelzése, egy számérték, amely például egy osztályozási vagy regressziós (közelítési) probléma megoldásaként jelenik meg.

Ez az ábra segít megérteni a neurális hálózatok alapvető működési elvét: a bemenetek fokozatos átalakulását a különböző rétegeken keresztül, amelyek végül egy konkrét kimeneti értékhez vezetnek. Ezt a folyamatot a gépi tanulás során finoman hangolják (optimalizálják), például visszaterjesztés (backpropagation) és gradienscsökkentés (gradient descent) segítségével, hogy a modell pontos előrejelzéseket tudjon adni.

Ha egy kép a bement, akkor a pixeleit sorban is be lehet adni a hálónak (nem vesszük figyelembe, hogy a kép téglalap). A finomhangolás során - a bemutatott minták alapján - a háló megtanulja a pixelek közötti összefüggéseket, és választ tud majd adni, hogy mosolyog-e a képen látható személy, egy olyan képen is, amit korábban nem mutattak meg a hálónak (a modellnek). Megjegyzés: olyan modellek természetesen jobban működnek, amik figyelembe veszik a szomszédos pixeleket is (pl. konvolúciós hálok).

Az ábrán, a fully-connected layer azt jelenti, hogy a minden bementi neuron minden a következő réteg minden neuronjával össze van kapcsolva.

A neurális hálót, az összeköttetéseihez rendelt súlyok segítségével tudjuk használni. A bementből és a rejtett réteg két neuronjának \(z_1\) és \(z_2\) értékét az alábbi képlettel számolhatjuk:

$$ z_1 = x_1 \cdot w_{11} + x_2 \cdot w_{21} $$ $$ z_2 = x_1 \cdot w_{12} + x_2 \cdot w_{22} $$

A rejtett réteg teljesen összekötött (fully connected), ezért minden bemenet kapcsolódik minden rejtett neuronhoz.

A következő kimeneti réteg \(z_3 = y_{pred}\) értékét, ami egyetlen neuronból áll így számíthatjuk:

$$ z_3 = z_1 \cdot w_{31} + z_2 \cdot w_{32} $$

Egyben ez lesz a háló előrejelzése \(y_{\text{pred}}\).

A fenti képleteket mátrixos és vektoros formában is felírhatjuk:

Rejtett réteg súlymátrixa: \( W_1 = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix}\)

A kimeneti réteg vektor: \( W_2 = \begin{bmatrix} w_{31} \\ w_{32} \end{bmatrix}\)

Bemeneti és rejtett réteg vektorok: \( \mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} , \quad \mathbf{z} = \begin{bmatrix} z_1 \\ z_2 \end{bmatrix}\)

Ezek alapján a rejtett réteget a bement és a súlymátrix alapján így számolhatjuk:

$$ \mathbf{z} = W_1 \cdot \mathbf{x} $$ behelyettesítve: $$ \begin{bmatrix} z_1 \\ z_2 \end{bmatrix} = \begin{bmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $$

A kimenet eredménye egy számérték (skalár) lesz:

$$ y_{\text{pred}} = \begin{bmatrix} w_{31} \\ w_{32} \end{bmatrix} \cdot \begin{bmatrix} z_1 \\ z_2 \end{bmatrix}$$

Teljes mátrixos formában:

$$ y_{\text{pred}} = W_2 \cdot W_1 \cdot \mathbf{x} $$

Tegyük fel hogy:

$$ W_1 = \begin{bmatrix} 0.5 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} , \quad W_2 = \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix} , \quad \mathbf{x} = \begin{bmatrix} 0.8 \\ 0.6 \end{bmatrix}$$

Rejtett réteg számítása:

$$ \mathbf{z} = \begin{bmatrix} 0.5 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} \cdot \begin{bmatrix} 0.8 \\ 0.6 \end{bmatrix} = \begin{bmatrix} (0.5 \cdot 0.8 + 0.3 \cdot 0.6) & (0.2 \cdot 0.8 + 0.7 \cdot 0.6) \end{bmatrix} = \begin{bmatrix} 0.58 \\ 0.58 \end{bmatrix}$$

Kimeneti réteg számítása:

$$ y_{\text{pred}} = \begin{bmatrix} 0.58 \\ 0.58 \end{bmatrix} \cdot \begin{bmatrix} 0.6 \\ 0.4 \end{bmatrix} = (0.52 \cdot 0.6 + 0.66 \cdot 0.4) = 0.58 $$

“Loss” a neurális háló teljesítményének mérésére szolgáló függvény, amely azt jelzi, hogy a háló által számolt kimenetek mennyire térnek el a várt kimenetektől.

$$ \text{Loss} = \frac{1}{2} (y - y_{pred})^2 $$

A back-propagation során a Loss függvény deriváltját (gradiensét) használjuk a súlyok frissítéséhez.

$$ \frac{\partial \text{Loss}}{\partial w_{31}} = \frac{\partial \text{Loss}}{\partial y_{\text{pred}}} \cdot \frac{\partial y_{\text{pred}}}{\partial w_{31}} $$

1.) Első tényező: \( \frac{\partial \text{Loss}}{\partial y_{\text{pred}}} \) a Loss függvény deriváltja a \(y_{pred}\)-re:

$$ \frac{\partial \text{Loss}}{\partial y_{\text{pred}}} = -(y_{\text{true}} - y_{\text{pred}}) = -e $$

ahol \( e = y - y_{\text{pred}} \) a hiba.

2.) Második tényező: \( \frac{\partial y_{\text{pred}}}{\partial w_{31}} \)

Az \(y_{pred}\) függ a rejtett kimenettől \(z_1\):

$$ y_{\text{pred}} = z_1 \cdot w_{31} + z_2 \cdot w_{32} $$

Ezért:

$$ \frac{\partial y_{\text{pred}}}{\partial w_{31}} = z_1 $$

Teljes derivált:

Összekapcsolva a két tényezőt:

$$ \frac{\partial \text{Loss}}{\partial w_{31}} = -e \cdot z_1 $$

hasonlóan:

$$ \frac{\partial \text{Loss}}{\partial w_{32}} = -e \cdot z_2 $$

3.) Gradiens a kimeneti súlyokra \(W_2\)

A súlyok gradiensének mátrixos formája:

$$ \Delta W_2 = \begin{bmatrix} \frac{\partial \text{Loss}}{\partial w_{31}} \\ \frac{\partial \text{Loss}}{\partial w_{32}} \end{bmatrix} = \begin{bmatrix} z_1 \cdot e \\ z_2 \cdot e \end{bmatrix}$$

A súlyok frissítését a gradiensek \(\Delta W_2\) és a tanulási ráta \(\eta\) segítségével frissítjük:

$$ W_2 = W_2 - \eta \cdot \Delta W_2 $$