Institute of Information Science - University of Miskolc

Kísérletek kimenetele, megfigyelések eredménye, rendszerek állapota, eseményteret alkot, amelyben véges vagy végtelen számosságú elemi esemény következhet be. A bekövetkezett események halmazokat alkotnak. Mivel az események halmazok, az eseményekkel halmazműveleteket végezhetünk. Az események bekövetkezése információt hordoz. Mindennapi tapasztalat szerint az események bekövetkezésének hírértéke nagyon különböző lehet.

Pl.: ha azzal a hírrel fogadnak, hogy 5 találatom van a lottón, ennek az információnak sokkal nagyobb a hírértéke, mint ha 1 találatom van.

Kísérletek kimenetelét megfigyelve azt tapasztaljuk, hogy az egyes események gyakorisága stabilitást mutat. Ha az $E$ eseménytérben $k$ számú megfigyelést végezve az $E_i$ esemény $k_i$-szer következett be, akkor az esemény $g_i$ gyakorisága: $g_i = \frac{k_i}{k}$.

Ez nem más, mint a $E_i$ esemény bekövetkezéseinek a száma $k_i$ osztva az összes elvégzett megfigyelés számával $k$.

Nagyszámú kísérlet esetén ez a gyakoriság, definíció szerint az $E_i$ esemény valószínűségéhez tart:

$\lim \limits_{k \to \infty} g_i = \frac {k_i}{k} = p(E_i) ,$

• ha $k_i = k$, akkor az esemény bekövetkezése biztos, azaz $p(E) = 1$
• ha $k_i = 0$, akkor az esemény bekövetkezése lehetetlen, azaz $p(E) = 0$

Az $E$ esemény $p(E)$ valószínűsége a bekövetkezés gyakoriságának mértéke.

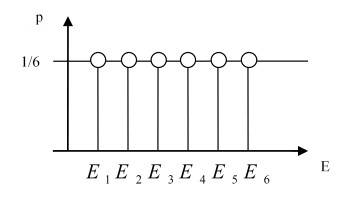
Pl.: a szabályos dobókocka feldobása, mint véletlen eseményhalmaz minden esemény egyhatod valószínűségű, amit ábrával is kifejezhetünk:

A kockadobás dobásai úgynevezett teljes eseményrendszert alkotnak. A teljes eseményrendszer fontos tulajdonsága, hogy az egyes események valószínűségeinek összege 1 és egy esemény bekövetkezése kizárja az összes többit.

$$\sum\limits_{i=1}^n p(E_i) = 1,$$