This is an old revision of the document!
Statisztikus tulajdonságok
Kísérletek kimenetele, megfigyelések eredménye, rendszerek állapota, eseményteret alkot, amelyben véges vagy végtelen számosságú elemi esemény következhet be. A bekövetkezett események halmazokat alkotnak. Mivel az események halmazok, az eseményekkel halmazműveleteket végezhetünk. Az események bekövetkezése információt hordoz. Mindennapi tapasztalat szerint az események bekövetkezésének hírértéke nagyon különböző lehet.
Pl.: ha azzal a hírrel fogadnak, hogy 5 találatom van a lottón, ennek az információnak sokkal nagyobb a hírértéke, mint ha 1 találatom van.
Kísérletek kimenetelét megfigyelve azt tapasztaljuk, hogy az egyes események gyakorisága stabilitást mutat. Ha az \(E\) eseménytérben \(k\) számú megfigyelést végezve az \(E_i\) esemény \(k_i\)-szer következett be, akkor az esemény \(g_i\) gyakorisága: \(g_i = \frac{k_i}{k}\).
Ez nem más, mint a \(E_i\) esemény bekövetkezéseinek a száma \(k_i\) osztva az összes elvégzett megfigyelés számával \(k\).
Nagyszámú kísérlet esetén ez a gyakoriság, definíció szerint az \( E_i \) esemény valószínűségéhez tart:
\( \lim \limits_{k \to \infty} g_i = \frac {k_i}{k} = p(E_i) , \)
- ha \(k_i = k \), akkor az esemény bekövetkezése biztos, azaz \( p(E) = 1 \)
- ha \(k_i = 0 \), akkor az esemény bekövetkezése lehetetlen, azaz \( p(E) = 0 \)
Az \( E \) esemény \(p(E)\) valószínűsége a bekövetkezés gyakoriságának mértéke.
Példa
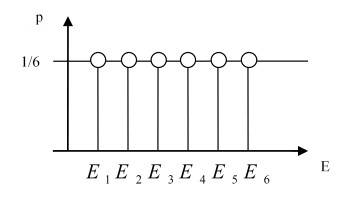
Pl.: a szabályos dobókocka feldobása, mint véletlen eseményhalmaz minden esemény egyhatod valószínűségű, amit ábrával is kifejezhetünk:
A kockadobás dobásai úgynevezett teljes eseményrendszert alkotnak. A teljes eseményrendszer fontos tulajdonsága, hogy az egyes események valószínűségeinek összege 1 és egy esemény bekövetkezése kizárja az összes többit.
$$ \sum\limits_{i=1}^n p(E_i) = 1, $$
ahol \( E_i \cap E_j = 0 \) és \( i \neq j \).
A kockadobás teljes eseményrendszerének halmaza hatféle, egyenként egyhatod valószínűségű eseményt tartalmaz. A kizárást az fejezi ki, hogy két különböző esemény metszete mindig 0.
Az összeg valószínűsége
Két fontos szabály, összetett események valószínűségével kapcsolatosan:
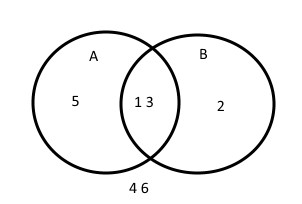
Feltehetjük a kérdést, hogy mekkora a valószínűsége két esemény valószínűségeinek az összege? Például mekkora a valószínűsége, hogy a dobókockával páratlant dobunk (A esemény) és annak, hogy négynél kisebbet dobunk (B esemény)?
A páratlan dobás valószínűsége három hatod, mert 6 esetből 3-szor tudunk páratlant dobni. Négynél kisebbet ugyancsak három hatod valószínűséggel dobhatunk hiszen itt az 1 és 2 és 3 dobása számít. Mondhatjuk tehát, hogy ezek szerint az összegzett valószínűség 1? Azaz a két esemény teljes eseményteret alkot?
Nem mondhatjuk. Mivel ha egyet és hármat dobunk, az mindkét eseményhez hozzátartozik.
Ha A és B eseménynek nem lenne közös halmaza, azaz egymást kizáró események lennének, akkor a
\( p( A \cup B) = p(A) + p(B) \)
Viszont általános képletet (képet) csak úgy alkothatunk, ha a két esemény metszetének valószínűségét levonjuk az összegből:
\( p( A \cup B) = p(A) + p(B) - p( A \cap B) \)
A képlet alapján a két esemény valószínűségének összege négy hatod.
Példa
Mekkora a valószínűsége annak, hogy egy kockával kétszer dobva mindkét esetben hatost dobunk?
A hatos dobás egyhatod valószínűségű, de nem vághatjuk rá, hogy összeadjuk kétszer és így kéthatod valószínűség lesz a megoldás. Ez azért van így, mert az események függetlenek. A két dobás között nincs összefüggés, független eseményeknek kell tekintenünk. Ilyenkor az eredmény a két esemény szorzata, azaz
\( p(A) \cdot p(B) = \frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36} \) lesz.