The outcome of experiments, the results of observations and the status of systems form a so-called 'event space', where finite or infinite cardinality elementary events may occur.

These events may form sets. Because they can be sets, we may perform set operations on them. When these operations occur, the event will carry information.

From everyday experience, the value of news about these events can be very different.

For example, if someone tells me that five of his numbers were drawn in the lottery, that information would be much more valuable than if they said only one number was drawn.

Observing the outcomes of these events, we may conclude that certain events show some stability in their frequency.

In the \( E_i \) event space, an event happened \(k_i\) times then the frequency of that given event may be calculated with the following formula:

\(g_i=\frac{k_i}{k} \)

This means that we divide the number of all events by the number (frequency) of that given event. In case of a large number of experiments this number will show us the probability of that event.

$$ \lim_{k \to \infty} g_i = \frac{k_i}{k} = P(E_i) $$

• if \(k_i = k \), then the occurrence will be certain \(P(E) = 1 \)

• if \(k_i = 0 \), then the occurrence will be impossible \(P(E) = 0 \)

The event's \(𝐸\) probability \(p(E)\) will be the occurrence's probability.

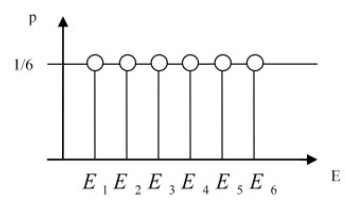
If we take the six-sided dice for our probability test the following will occur:

The probability of every event will be 1/6 which can be calculated with the following formula. The rolls (of the dice) will form a so-called full event system. In the case of a full event system the sum of the probabilities (of each event) is 1 by definition.

If one the events happen then the others can not happen:

$$ \sum_{i=1}^{n} p(E_i) = 1 \text{ where } E_i \cap E_j = 0 \text{ and } i \not = j $$

This formula applies to a set of mutually exclusive events. Since these events are disjoint (no overlap between any two different events) and together they cover all possible outcomes (the sum of their probabilities is 1).

What is the sum of two different events' probability?

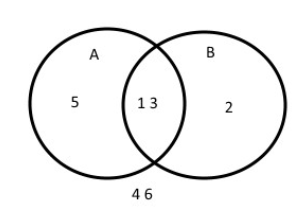
Example 1: what is the probability that we throw an odd number (with a dice) (Event A) and a number less then 4 (Event B)?

If A and B event would not have common events (so that they would exclude each other) the formula would be the following: \( p(A \cup B) = p(A) + p(B) \).

We can only form a general formula, if we extract the probability of the intersection of both sets from the total sum:

$$ p(A \cap B) = p(A) + p(B) - p(A \cup B) $$

So we can say that (according to this formula) the total probability for both events is 4/6.

Example 2: What is the probability that we roll the dice twice and the results will be 6 in both cases?

The probability for throwing a 6 is 1/6, but we cannot multiply it by 2 and take the result (2/6). We can not do that because both events are independent. There is no connection between the 2 trials, so we have to look at them as independent events. So the result will be the multiplication of both events:

$$ p(A) p(B) = \frac{1}{6} \frac{1}{6} = \frac{1}{36} $$