Institute of Information Science - University of Miskolc

Hétköznapi szóhasználatban a tanulás azt jelenti, hogy egy feladat megoldásához szabályokat találunk, vagy fedezünk fel. Például egy kisgyermek megtanulhatja, hogy a madaraknak van szárnyuk, és képesek repülni – anélkül, hogy ezt valaki pontos szabályok formájában elmagyarázná neki. A gyerek megfigyelései alapján felismeri a jellemző mintákat és kapcsolatokat, és ez alapján képes új esetekre is következtetni.

Formálisan tekintve, a gépi tanulás célja olyan függvény megtalálása, amely egy bemeneti adat 𝑥 alapján megbízhatóan becsli a hozzá tartozó kimenetet 𝑦. Például ha a bemenet egy rendszámtáblát ábrázoló kép, a kimenet a rajta olvasható szöveg lesz.

Ahhoz, hogy ez megvalósuljon, először is összegyűjtünk egy tanítóhalmazt, amely bemeneti és kimeneti adatpárokat tartalmaz:

$$ \mathcal{D} = \{(x_1, y_1), (x_2, y_2), \ldots, (x_N, y_N)\} $$

Ezután definiálunk egy paraméteres modellt \( f(x; w) \), ahol:

• \( f \) egy függvény (pl. neurális hálózat),
• \( w \) a tanulható paraméterek összessége (súlyok),

cél, hogy \( f(x_i; w) \approx y_i \) legyen, azaz tetszőlegesen kiválasztott adatpár bemenetére \(x_i\), az \(y_i\) kimenetet adja.

A tanulás célja az optimális \( w^* \) paraméter megtalálása, amely mellett a modell jól teljesít. A modell jóságát (teljesítményét) veszteségfüggvény segítségével mérjük:

$$ \mathcal{L}(w) = \frac{1}{N} \sum_{n=1}^N \ell(y_n, f(x_n; w)) $$

ahol \( \ell \) például lehet a négyzetes hiba, aminek egyik bemenete a tanító halmaz \(y\) kimenetének értékéből kivonja, a modell által számolt \(\hat{y}\) kimenetet és ennek a különbségnek veszi a négyezetét:

$$ \ell(y, \hat{y}) = (y - \hat{y})^2 $$

Ilyenkor a \( \ell \) veszteségfüggvény értéke a négyzetes hibák átlaga. Behelyettesítve:

$$ \mathcal{L}(w) = \frac{1}{N} \sum_{n=1}^N (y_n - f(x_n; w))^2 $$

A tanulás célja, hogy megtaláljuk azt a paraméterbeállítást, amely a lehető legjobban teljesít. Ez azt jelenti, hogy olyan súlyokat (paramétereket) keresünk, amelyek a lehető legkisebb hibát eredményezik a tanítóadatokon.

Másként fogalmazva: a tanulás során azt a súlyvektort szeretnénk megtalálni \(w^*\), amely minimalizálja a veszteségfüggvényt — vagyis azt, amely mellett a modell becslései a lehető legközelebb esnek a tényleges válaszokhoz az összes tanítópéldára nézve.

$$ w^* = \arg\min_w \mathcal{L}(w) $$

Ez a megközelítés számos alkalmazás alapját képezi: képfelismerés, szövegértés, hangfeldolgozás, játékstratégia stb. A modell nem szabályokat programozva működik, hanem adatokból „tanul meg” viselkedni.

Tegyük fel, hogy a modellünk (becslő függvény) így néz ki:

$$ f(x; w) = wx $$

és két tanítópéldánk van:

• (1, 2)
• (2, 4)

A cél, hogy olyan \( w \) súlyt találjunk, amely a következő veszteségfüggvényt minimalizálja:

$$ \mathcal{L}(w) = \frac{1}{2}[(2 - w \cdot 1)^2 + (4 - w \cdot 2)^2] $$

Ez a függvény azt méri, hogy adott \( w \) esetén mekkora hibát követ el a modell. Az alábbi ábrán látható a veszteségfüggvény alakja, valamint a minimumhely:

• A minimális veszteség \( \mathcal{L}(w) \approx 0.00 \)
• A hozzá tartozó optimális súly: \( w^* = 2.01 \)

Legyen a modell több paraméteres:

$$f(x; w) = \sum_{k=1}^K w_k f_k(x)$$

ahol:

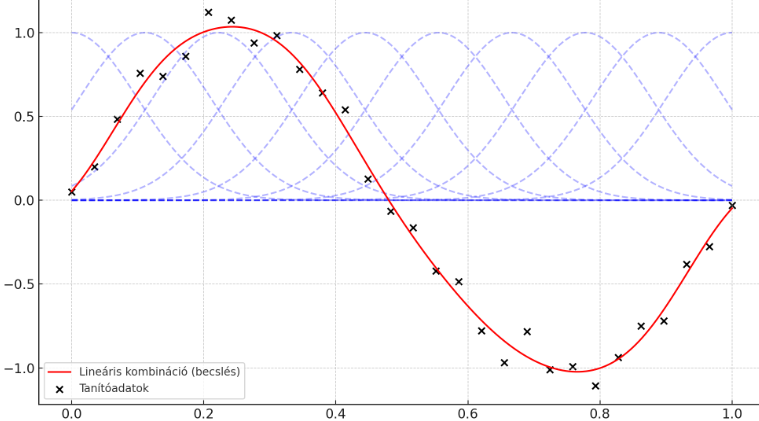
• \(f_k(x)\) előre definiált bázisfüggvények (pl. Gauss-görbék, szinuszok, polinomok stb.)

• Fekete pontok: zajos tanítóadatok \( (x_n, y_n) \)
• Kék görbék: a 10 darab Gauss-alakú bázisfüggvény \(f_k(x)\)
• Piros görbe: a tanult függvény \( f(x; w^*) = \sum w_k f_k(x) \)

A modell megtanulta, milyen súlyokkal (\(w\)-kel) kombinálja a bázisfüggvényeket úgy, hogy a piros görbe minél jobban kövesse a tanítóadatokat, azaz minimalizálja a négyzetes hibát.

A következő Python program hozta létre a fenti ábrát.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from scipy.linalg import solve

# 1. Tanítóadat generálása (zajos szinuszgörbe)
np.random.seed(42)
N = 30
x_train = np.linspace(0, 1, N)
y_train = np.sin(2 * np.pi * x_train) + 0.1 * np.random.randn(N)

# 2. Bázisfüggvények: Gauss-görbék
K = 10  # Bázisfüggvények száma
centers = np.linspace(0, 1, K)
width = 0.1

def gaussian_basis(x, c, s):
    return np.exp(-0.5 * ((x - c)/s)**2)

# 3. Design mátrix Φ (N x K)
Phi = np.stack([gaussian_basis(x_train, c, width) for c in centers], axis=1)

# 4. Optimális súlyok kiszámítása (normálegyenlet)
#  Φ w = y  => w = (ΦᵗΦ)⁻¹ Φᵗ y
w_star = solve(Phi.T @ Phi, Phi.T @ y_train)

# 5. Kiértékelés új pontokon
x_test = np.linspace(0, 1, 200)
Phi_test = np.stack([gaussian_basis(x_test, c, width) for c in centers], axis=1)
y_pred = Phi_test @ w_star

# 6. Eredmény kirajzolása
plt.figure(figsize=(10, 6))
for k in range(K):
    plt.plot(x_test, Phi_test[:, k], '--', color='blue', alpha=0.3)  # bázisfüggvények

plt.plot(x_test, y_pred, color='red', label='Lineáris kombináció (becslés)')
plt.scatter(x_train, y_train, color='black', label='Tanítóadatok')
plt.title("Basis function regression Gaussian bázisfüggvényekkel")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

A modell kapacitása és a rendelkezésre álló tanítóadatok mennyiségének viszonya fontos szerepet játszik a tanulás sikerességében.

Ha a modell túl egyszerű (kevés paramétert vagy kevés bázisfüggvényt használ), akkor nem lesz elég rugalmas ahhoz, hogy megtanulja az adatok mögötti összefüggéseket. Ez az eset az underfitting (gyenge illeszkedés): a modell nem tud alkalmazkodni még a tanítóadatokhoz sem, és mind a tanító-, mind a tesztpéldákon nagy hibát vét.

Ezzel szemben, ha a modell túl bonyolult (pl. túl sok paraméterrel dolgozik), akkor hajlamos arra, hogy a tanítóadatokra túlzottan “ráilleszkedjen”. Ez az overfitting (túlzott illeszkedés), amely során a modell tökéletesen teljesít a tanítóhalmazon, de új, ismeretlen adatokra gyengén általánosít. Megtanulja a tanító halmazban lévő “zajt”, pl. az esetleges hibás vagy kiugró értékeket is.

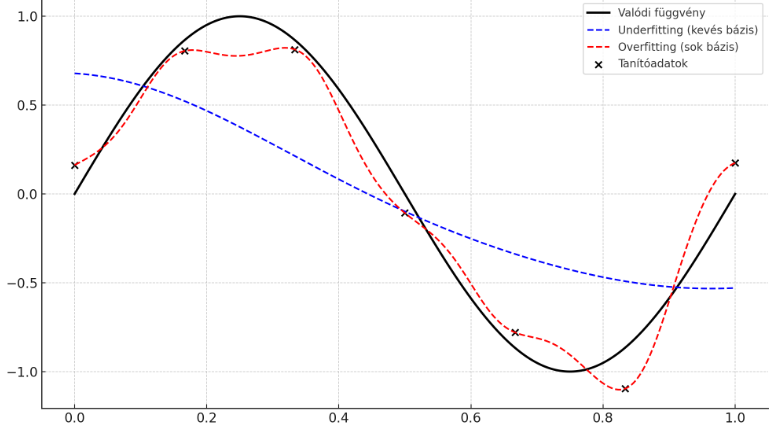
Az alábbi ábra ezt a jelenséget szemlélteti:

• A fekete vonal a valódi (ismeretlen) függvény, amely szerint az adatok keletkeztek.
• A fekete pontok a tanítópéldák.
• A kék szaggatott görbe egy túl egyszerű modell (underfitting): nem tudja követni a mintát.
• A piros szaggatott görbe egy túltanult modell (overfitting): jól illeszkedik a pontokra, de a valódi görbétől eltér.

Olyan modellt érdemes tervezni, amely épp elég rugalmas ahhoz, hogy meg tudja tanulni az adatok szerkezetét, de nem annyira rugalmas, hogy a véletlen zajokat is megtanulja.

A következő program hozza létre a fenti ábrát:

import numpy as np
import matplotlib.pyplot as plt

# Valódi (rejtett) függvény
def true_function(x):
    return np.sin(2 * np.pi * x)

# Tanítóadat
np.random.seed(1)
x_train = np.linspace(0, 1, 7)
y_train = true_function(x_train) + 0.1 * np.random.randn(len(x_train))

# Teszteléshez sűrű intervallum
x_test = np.linspace(0, 1, 300)
y_true = true_function(x_test)

# Gauss bázisfüggvények
def gaussian_basis(x, c, s):
    return np.exp(-0.5 * ((x - c)/s)**2)

def design_matrix(x, centers, width):
    return np.stack([gaussian_basis(x, c, width) for c in centers], axis=1)

# Underfitting (kevés bázis)
centers_under = np.linspace(0, 1, 3)
Phi_under = design_matrix(x_train, centers_under, 0.3)
Phi_under_test = design_matrix(x_test, centers_under, 0.3)
w_under = np.linalg.lstsq(Phi_under, y_train, rcond=None)[0]
y_under_pred = Phi_under_test @ w_under

# Overfitting (sok bázis)
centers_over = np.linspace(0, 1, 15)
Phi_over = design_matrix(x_train, centers_over, 0.05)
Phi_over_test = design_matrix(x_test, centers_over, 0.05)
w_over = np.linalg.lstsq(Phi_over, y_train, rcond=None)[0]
y_over_pred = Phi_over_test @ w_over

# Ábra
plt.figure(figsize=(10, 6))
plt.plot(x_test, y_true, color='black', linewidth=2, label='Valódi függvény')
plt.plot(x_test, y_under_pred, color='blue', linestyle='--', label='Underfitting (kevés bázis)')
plt.plot(x_test, y_over_pred, color='red', linestyle='--', label='Overfitting (sok bázis)')
plt.scatter(x_train, y_train, color='black', label='Tanítóadatok')
plt.title("Underfitting és overfitting példája")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

A gépi tanulási modelleket három nagy csoportba sorolhatjuk a tanulás célja és a kimenet jellege alapján:

A regressziós feladat célja egy folytonos mennyiség becslése. Ilyenkor a modell egy bemenethez \( x \in \mathbb{R}^d \) tartozó kimeneti értéket \( y \in \mathbb{R}^k \) próbál megjósolni.

Példák:

• Egy tárgy térbeli pozíciójának becslése egy képből.
• Egy hőmérséklet vagy ház árának előrejelzése.

Osztályozás során a cél az, hogy a modell egy véges számú lehetséges címke (osztály) közül válasszon ki egyet egy adott bemenethez. Azaz:

$$ y \in \{1, 2, \ldots, C\} $$

A modell általában nem közvetlenül egy címkét ad vissza, hanem pontszámokat vagy valószínűségeket rendel minden lehetséges osztályhoz:

$$ f(x; w) = \text{softmax}(s_1, s_2, \ldots, s_C) $$

ahol \( s_i \) a \( i \)-edik osztályhoz tartozó nyers pontszám. A predikció:

$$ \hat{y} = \arg\max_{i} f_i(x; w) $$

A tanítóadat itt is \( (x_n, y_n) \) párokból áll, de a \( y_n \) most egy osztályindex.

A harmadik kategória a sűrűségmodellezés, amelynek célja nem kimeneti érték előrejelzése, hanem magának az adatnak a valószínűségi eloszlását megtanulni:

$$ p(x) \approx \hat{p}(x; w) $$

Ilyenkor csak \( x_n \) példák állnak rendelkezésre (nincs hozzájuk tartozó \( y_n \)), és a modell azt próbálja megtanulni, mennyire jellemzőek az egyes minták, vagy hogyan lehet új mintákat generálni az eloszlásból.

Jellegzetes célfüggvény itt az eloszlás log-likelihood maximálása:

$$ \mathcal{L}(w) = -\frac{1}{N} \sum_{n=1}^N \log \hat{p}(x_n; w) $$

• A regresszió és osztályozás esetén mindig szükség van egy célértékre (\( y \)), ezért ezeket felügyelt tanulásnak nevezzük.
• A sűrűségmodellezés során nincs célérték, csak maga az \( x \) szerepel, ezért ez a felügyelet nélküli tanulás kategóriájába soroljuk.

Ezek a kategóriák nem zárják ki egymást. Például:

• Osztályozás megvalósítható regressziós formában is (pontszámokat tanulunk).
• Sűrűségmodellezésből származtathatunk osztályozót (pl. Bayes-szabály szerint).
• Léteznek összetett modellek, amelyek többféle célt is egyszerre tanulnak (pl. képgenerálás és címkézés együtt).

A modern gépi tanulási modellek gyakorlati megvalósítása és alkalmazása, szorosan összefügg a hatékony számítási megoldásokkal. Ezek a modellek hatalmas adathalmazokon dolgoznak, így a háttérben zajló számításokat olyan eszközökön érdemes végrehajtani, amelyek párhuzamosan képesek nagy mennyiségű művelet elvégzésére.

A legtöbb mélytanulási számítás grafikus feldolgozóegységek (GPU-k) segítségével történik. Ezeket eredetileg képfeldolgozásra tervezték, de mivel képesek több ezer szálon párhuzamos számításokat végezni, kiválóan alkalmasak a gépi tanulás modelljeinek betanítására és futtatására is.

A GPU-k saját gyors memóriával rendelkeznek, amelyben az adatokat és a modell súlyait is tárolni lehet. A legnagyobb lassulást (szűk keresztmetszet) általában az okozza, ha az adatokat a CPU memóriájából át kell másolni a GPU-ba. Ezért fontos, hogy a számításokat úgy szervezzük, hogy az adatok a GPU memóriájában maradjanak.

A hatékony működés érdekében az adatokat gyakran batch-ekre (kötegekre) osztjuk, vagyis egyszerre több mintát dolgozunk fel. A GPU szinte ugyanolyan gyorsan képes feldolgozni egy batch-et, mint egyetlen mintát, mivel a szűk keresztmetszet ilyenkor is a GPU-ba történő adatbetöltés marad.

Egy tipikus GPU elméleti teljesítménye:

$$ 10^{13} \text{ – } 10^{14} \text{ FLOP/s (floating point művelet másodpercenként)} $$

A lebegőpontos számokat jellemzően 32 biten (FP32) tároljuk, de sok esetben 16 bites (FP16) vagy kisebb pontosság is elegendő, ami még tovább gyorsíthatja a számítást. FP16-os tárolással közel kétszeres sebességnövekedés érhető el, az FP32-vel szemben.

A mélytanulási könyvtárak, mint a PyTorch vagy a JAX, a számításokat tenzorokkal végzik. Egy tenzor nem más, mint egy tömb, amely elemei (számok) több dimenzió mentén vannak elrendezve. A vektorok és mátrixok a tenzorok speciális esetei:

$$ \text{Vektor: } \mathbb{R}^n, \quad \text{Mátrix: } \mathbb{R}^{n \times m}, \quad \text{Tenzor: } \mathbb{R}^{N_1 \times N_2 \times \dots \times N_k} $$

A tenzorokkal reprezentáljuk:

• a bemeneti adatokat (pl. képek, hangminták),
• a modell paramétereit (súlyok),
• a rejtett rétegek aktivációit.

Példák:

• Egy RGB kép (64 pixel × 64 pixel): \( \mathbb{R}^{3 \times 64 \times 64} \)
• 32 ilyen kép: \( \mathbb{R}^{32 \times 3 \times 64 \times 64} \)

A népszerű mélytanulási könyvtárak lehetővé teszik ezek formátumának gyors átalakítását (tenzorátalakításokat).

Ha van egy mátrixunk:

$$ A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \in \mathbb{R}^{2 \times 3} $$

A transzponáltja:

$$ A^\top = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix} \in \mathbb{R}^{3 \times 2} $$

PyTorch-ban:

A = torch.tensor([[1, 2, 3],
                  [4, 5, 6]])
A_T = A.T  # vagy A.transpose(0, 1)

Tegyük fel, hogy van egy 3×4-es mátrix, és csak az első két oszlopra van szükségünk:

$$ B = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \end{bmatrix} $$

Kivágva az első két oszlop:

$$ B[:, 0:2] = \begin{bmatrix} 1 & 2 \\ 5 & 6 \\ 9 & 10 \end{bmatrix} $$

PyTorch-ban:

B = torch.arange(1, 13).reshape(3, 4)
slice = B[:, 0:2]  # minden sor, az első két oszlop

Egy hosszú vektor:

$$ v = [1, 2, 3, 4, 5, 6] \in \mathbb{R}^6 $$

Ezt átalakíthatjuk egy 2 soros, 3 oszlopos mátrixszá:

$$ \text{reshape: } \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \in \mathbb{R}^{2 \times 3} $$

PyTorch-ban:

v = torch.tensor([1, 2, 3, 4, 5, 6])
reshaped = v.reshape(2, 3)

Ezek a műveletek gyakran memóriamásolás nélkül végrehajthatók, ami különösen hatékonnyá teszi őket. A modern mélytanulási rendszerek tervezése során a tenzoros reprezentáció fontos követelmén. Ha a számításokat tenzoros formában szervezzük meg, akkor ez lehetővé teszi a hatékony párhuzamos végrehajtást. Minden szint – a modell, a programkönyvtár, a hardver – kompatibilis kell legyen ezzel a reprezentációval. A tenzoros struktúra támogatja a memóriabeli lokalitást, vagyis a gyakran használt adatok közel maradnak egymáshoz a memóriában, ezáltal gyorsabb az elérésük.