Hamming távolság
A redundancia növelésével automatikus hibajavítás is végezhető. Ha m adatbitünk van, akkor ehhez rendeljünk r darab redundáns paritásbitet, így a teljes bithossz n:
$$ n = m + r. $$
Ha adott két kódszó, pl: 00101110 és 00111110 és ezek 1 bitben térnek el egymástól, akkor a kódszavak Hamming távolsága 1.
Ez egy érdekes távolság fajta, mert nem függ attól, hogy a hányadik bit különbözik, és attól sem, hogy ezen a helyen bináris vagy tízes számrendszerbeli szám áll. Tehát pl. 45635263 és 45615263 két szónak is 1 a Hamming távolsága, hiába a hibás helyen még 8-féle más szimbólum is állhatna!
Ennek az a jelentősége, hogy ha két kódszó távolsága d, akkor d darab egyszeres bithibának kell lennie ahhoz, hogy az egyik kódszó a másikba alakulhasson.
Például az 11110001 és a 00110000 Hamming távolsága 3, mert 3 egyszeres bithiba szükséges ahhoz, hogy az egyik a másikba alakulhasson.
d egyszeres bithiba felismeréséhez \(d + 1\) távolságú kódolás kell, mert ebben az esetben d egyszeres bithiba semmiféleképpen nem alakíthat át egy érvényes kódszót egy másik érvényes kódszóvá.
Az egyszeres bithibák javításához a Hamming-kódokban szükséges paritásbitek számát a következőképpen lehet meghatározni:
Ha a kódolt üzenet m adatbitet tartalmaz, akkor legalább r paritásbit szükséges, ahol r olyan, hogy teljesüljön az egyenlőtlenség:
$$ 2^r \geq m + r + 1. $$ $$ 2^r \geq n + 1. $$
Ez azt jelenti, hogy az r paritásbitnek képesnek kell lennie megkülönböztetni a \(m+r+1\) különböző állapotot (beleértve a hibamentes állapotot és az összes lehetséges hibás bitpozíciót).
Ha \( m = 8 \) adatbitet akarunk egyszeres bithibajavítással kódolni, akkor nézzük meg, hány paritásbitre van szükségünk a fenti egyenlőtlenség alapján:
Próbáljuk meg meghatározni \( r \)-t különböző értékekkel:
\( r = 3 \): \[ 2^3 = 8 \quad \text{és} \quad m + r + 1 = 8 + 3 + 1 = 12 \] Ez nem elég, mert \( 8 < 12 \), tehát 3 paritásbit nem elegendő.
\( r = 4 \): \[ 2^4 = 16 \quad \text{és} \quad m + r + 1 = 8 + 4 + 1 = 13 \] Ez kielégíti az egyenlőtlenséget, mivel \( 16 \geq 13 \), tehát 4 paritásbit elegendő ahhoz, hogy 8 adatbit esetén egyszeres bithibát javítsunk.
Tehát 8 adatbit esetén 4 paritásbit szükséges az egyszeres bithibák javításához.
A következő táblázatban kiszámítottuk több bithosszra:
| Szó hossza (m) | Paritásbitek száma ® | teljes bithossz (m+r = n) | hozzáadott bitek %-a |
|---|---|---|---|
| 8 | 4 | 12 | 50 |
| 16 | 5 | 21 | 31 |
| 32 | 6 | 38 | 19 |
| 64 | 7 | 71 | 11 |
| 128 | 8 | 136 | 6 |
| 256 | 9 | 265 | 4 |
| 512 | 10 | 522 | 2 |
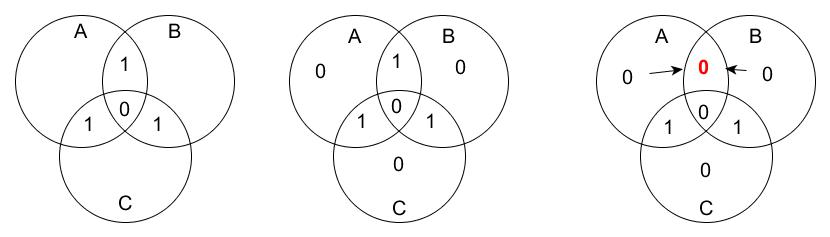
Bithibák automatikus javításának elve a következő ábra alapján értelmezhető:
Kódoljuk az 1101 üzenetet, képezzünk három halmazt A, B, C és a halmazok AC, AB, ABC, BC közös részeibe írjuk be a biteket. A középső ábrán pedig írjuk be a 3 paritásbitet a halmazokba. A harmadik képen azt mutatjuk be, hogyha hibás bit érkezik, akkor a paritás ellenőrzés megmutatja melyik metszetben van rossz érték.