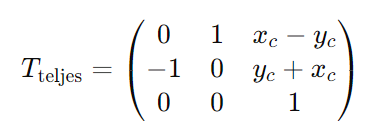Institute of Information Science - University of Miskolc

A koordináták felcserélését közvetlenül elvégezhetjük a következő 2×2-es mátrix alkalmazásával:

$$ M = \left[\begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix}\right] $$

Ez a mátrix az alábbiak szerint működik:

$$ \left[\begin{matrix} 0 & 1 \\ 1 & 0 \\ \end{matrix}\right] \left[\begin{matrix} x \\ y \\ \end{matrix}\right] = \left[\begin{matrix} y \\ x \\ \end{matrix}\right] $$

Az eltolás, vagy transzláció, egy geometriai objektum helyzetének megváltoztatása a síkon anélkül, hogy forgatnánk, méreteznénk, vagy torzítanánk azt. Egy pont, vagy egy objektum x,y koordinátáinak eltolásához $t_x$ és $t_y$ értékekkel: $​x$ és $y$ tengelyek mentén, a következő transzformációs mátrixot használjuk:

$$ T = \left[ \begin{array}{cc|c} 1&0&t_x\\ 0&1&t_y\\ 0&0&1 \end{array} \right] $$

Ez a mátrix homogén koordinátákat használ, ami lehetővé teszi az eltolások, forgatások és más transzformációk kombinálását egyetlen műveletben. A transzformáció során egy pont P(x,y) homogén koordinátái P(x,y,1) lesznek, és az eltolás utáni koordináták a következőképpen számolhatók ki:

$$ \left[\begin{matrix} 0 & 1 & t_x\\ 1 & 0 & t_y\\ 0 & 0 & 1 \end{matrix}\right] \left[\begin{matrix} x \\ y \\ 1 \end{matrix}\right] = \left[\begin{matrix} x + t_x \\ y + t_y \\ 1 \end{matrix}\right] $$

Amikor egy pontot vagy objektumot szeretnénk 90 fokkal az óramutató járásával megegyezően elforgatni egy adott pont körül, a transzformációt három lépésre bonthatjuk:

1. Eltolás, hogy a forgatási középpont az origóba kerüljön.
2. Forgatás 90 fokkal az óramutató járása szerint.
3. Visszatolás a forgatási középpont eredeti helyére.

Ezeket a lépéseket egyetlen 3×3-as transzformációs mátrixszal kombinálhatjuk, amely így néz ki:

1. Előkészítés eltolással:
2. 90 fokos forgatás:
3. Visszatolás:

A teljes transzformációs mátrix, , a következőképpen számítható:

Ami egyenlő: