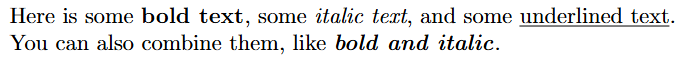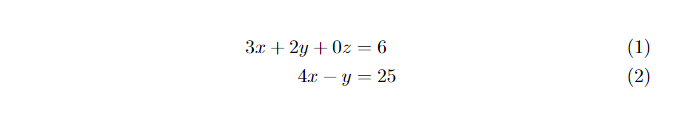Institute of Information Science - University of Miskolc

The goal of the lesson is to become familiar with LaTeX, specifically for the purpose of writing mathematical expressions.

What is LaTeX?

LaTeX is a high-quality typesetting system, primarily used for technical and scientific documents. It is particularly powerful for formatting complex mathematical equations and formulas, making it a preferred choice in academia and research.

What are the advantages of LaTeX?

• Handling Complex Documents: It is ideal for mathematical formulas, citations, and cross-referencing in technical writing.
• Consistent Layout: Automatically ensures a uniform, professional design by separating content from formatting.
• Scalability: Suitable for large projects, allowing version control and modular structure.
• Longevity: LaTeX's plain text format ensures long-term compatibility and durability.
• Academic Preference: Often required in academic and scientific publishing.

Getting Started:

1. Overleaf: We will use Overleaf, a free online LaTeX editor, which allows you to write and compile LaTeX documents directly in your browser.
   1. Sign up at Overleaf.
   2. Overleaf offers collaborative features, version control, and a vast library of LaTeX templates.

Basic Document Structure:

\documentclass{article}  % Specifies the document class (article, report, book, etc.)
\begin{document}          % Begins the content of the document
% Your content goes here
\end{document}            % Ends the content of the document

1. \documentclass{article}: Defines the overall layout and style of the document.
2. \begin{document} and \end{document}: Everything between these commands will be included in the output document.

1. Inline Math: For mathematical expressions that appear within a line of text, use $…$.
   1. E.g. $E = mc^2$ is written as $E = mc^2$ in LaTeX.
2. Display Math: For standalone equations, use $$…$$.
   1. E.g. To display $$E = mc^2$$ on its own line, use $$E = mc^2$$.

\documentclass{article}
\begin{document}
 
The equation $E = mc^2$ is famous in physics. It is so important that we can highlight $$E = mc^2$$ by putting it to a separate line.
 
\end{document}

This code will became:

1. Exponents (superscripts): Use ^ for superscripts.
   1. E.g. $x^2$ is written as $x^2$.
2. Subscripts: Use `_` for subscripts.
   1. E.g. $a_1$ is written as $a_1$.
3. Fractions: Use `\frac{numerator}{denominator}`.
   1. E.g. $\frac{a}{b}$ is written as $\frac{a}{b}$.

\documentclass{article}
\begin{document}
 
% Exponent and subscript
The formula for the area of a circle is $A = \pi r^2$.
 
% Fraction
The equation $\frac{a}{b} = c$ represents a fraction.
 
% Combined
The equation for kinetic energy is $K = \frac{1}{2}mv^2$.
 
\end{document}

This code will become:

LaTeX provides a variety of symbols to accurately represent mathematical expressions.

1. The plus-minus symbol is used to denote values that can be either positive or negative and is written as \pm, which displays as $\pm$.
2. To express square roots, the square root symbol is used, which is written as \sqrt{…}. For example, \sqrt{2} produces $\sqrt{2}$
3. For higher-order roots, such as a cubic root, the syntax is \sqrt[3]{…}, yielding $\sqrt[3]{9}$
4. Another common symbol is the infinity symbol, represented as \infty, and it is displayed as $\infty$
5. For greater than or equal to and less than or equal to symbols, use \geq and \leq, which render as $\geq$ and $\leq$, respectively.

The general form of summation in LaTeX is written using the \sum command. For example, the sum from $i=1$ to $n$ is given by:

$$\sum_{i=1}^{n} i^2$$

This expression sums the squares of integers from 1 to $n$.

The derivative of a function $f(x)$ with respect to $x$ is represented in LaTeX using the \frac command for fractions. The notation for the derivative of $f(x)$ with respect to $x$ is:

$$\frac{d}{dx} f(x)$$

This gives the rate of change of $f(x)$ with respect to $x$.

For partial derivatives, the \partial command is used. The partial derivative of a function $f(x, y)$ with respect to $x$ is:

$$\frac{\partial}{\partial x} f(x, y)$$

This expression gives the partial derivative of $f$ with respect to $x$, holding other variables constant.

Partial integration, also known as integration by parts, can be expressed in LaTeX. For the specific example of integrating $x \sin(x)$ from $a$ to $b$, the integral is written as:

\[ \int_{a}^{b} x \sin(x) \, dx \]

This represents the definite integral of $x \sin(x)$ with respect to $x$ from $a$ to $b$.

1. The `align` environment is used to align multiple equations. Each line of the equation is aligned using the `&` symbol, typically before the equal sign or any other operator.
2. Use `\\` to separate lines.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
 
\begin{align}
  3x + 2y + 0z &= 6 \\
  4x - y &= 25
\end{align}
 
\end{document}

This code will become:

Explanation:

1. \usepackage{amsmath}: The `amsmath` package is required for advanced mathematical typesetting features, including the `align` environment.
2. &: This symbol is used to align equations at the specified point, usually before an operator like `=`.

Tips:

1. You can label equations using the \label{} command and refer to them later with \ref{}.
2. Example:

\begin{equation} \label{eq:quadratic}
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\end{equation}

To refer to this equation later, use Equation \ref{eq:quadratic}.

Reproduce the following mathematical proof in LaTeX. Use inline and display math, as well as basic and special symbols! Save the result in PDF format!

Raw text:

Proof: √2 is Irrational

Assume, for contradiction, that 2 is rational. Then it can be expressed as a fraction a/b, where a and b are coprime integers.

Then:
HERE COMES AN EQUATION.

Squaring both sides:
HERE COMES AN EQUATION.

Multiplying both sides by b2:
HERE COMES AN EQUATION.

This implies that a2 is even, so a must also be even. Let a = 2k for some integer k.

Substituting into the equation:
HERE COMES AN EQUATION.

Dividing by 2:
HERE COMES AN EQUATION.

This implies that b2 is even, so b must also be even.

But if both a and b are even, they are not coprime, which contradicts our original assumption. Therefore, 2 must be irrational.